Пуассоновский поток событий

Среди потоков событий особое место занимает так называемый «пуассоновский поток», обладающий по сравнению с другими, рядом свойств, существенно облегчающих решение задач.

Пуассоновским потоком событий называется поток, обладающий двумя свойствами – ординарностью и отсутствием последствий.

Поток называется потоком без последействия, если для любых двух не перекрывающих участков t₁ и t₂ число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.

Рис. 2.4

Обозначили случайное число событий, наступивших на интервале времени t₁,через х ₁ и на интервале t₂, через х ₁₂. Для потока без последействия случайные величины х ₁ и х ₂ независимы, т.е. вероятность того, что на участке t₂ наступило определенное число событий m ₂ не зависит от того, сколько событий m₁ наступило на участке t₁.

P (x ₂= m ₂½ x ₁= m ₁) = P (x ₂= m).

(m ₁ =0, 1, 2,…)

(m ₂ =0, 1, 2,…). (2.47)

Из теории вероятностей известно, что для пуассоновского потока число событий х ₁, попадающих на любой интервал длины t, примыкающих к точке t, распределено по закону Пуассона (рис. 2.5.):

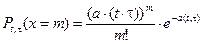, (2.48)

где (а× (t× t)) ^m – среднее число событий, наступающих на интервале времени t, примыкающем к моменту времени t. Поэтому поток и называется «пуассоновским».

Рис. 2.5

Среднее число событий для ординарного потока равно интенсивности потока l(t). Следовательно, среднее число событий наступающих на интервале времени t, примыкающем к моменту времени t будет равно:

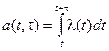. (2.49)

Если пуассоновский поток событий является стационарным [l(t) = l = const], то величина а не будет зависеть от t:

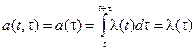. (2.50)

В этом случае вероятность того, что на произвольно выбранном участке времени продолжительностью t наступит m событий, определяется по формуле:

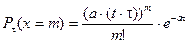. (2.51)

Стационарный поток часто называется простейшим потоком, поскольку применение простейших потоков при анализе различных систем массового обслуживания приводит к наиболее простым решениям. Найдем закон распределения интервала времени между двумя событиями в простейшем потоке (рис 2.6.):

Рис. 2.6

Вероятность того, что на участке t, следующем за одним событием не появится не одного события будет:

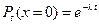. (2.52)

Но эта вероятность равна вероятности того, что случайные величины Т будут больше величины t. Следовательно,

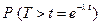, (2.53)

откуда

F (t)= P (T <1)=1 - p ×(T > t)=1 - e^-lt, t >0. (2.54)

где F (t) –функция распределения случайной величины Т.

Дифференцируя это выражение, получим плотность распределения случайной величины Т:

f (t)=l e^-lt, (t >0). (2.55)

Таким образом, в простейшем потоке интервалы между двумя соседними событиями распределен по доказательному закону с параметром l.

Вследствие отсутствия последействия все интервалы между соседними событиями представляют собой независимые случайные величины. Поэтому простейший поток представляет собой стационарный поток Пальма.

Математическое ожидание и дисперсия случайной величины Т -интервала времени между двумя событиями в простейшем потоке, равны:

Таким образом,

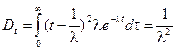; (2.56)

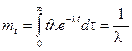. (2.57)

Регулярный поток событий:

; , (2.58)

где Т* участок, на который упадает случайное событие.

Регулярный поток представляет собой последовательность событий, разделенных строго одинаковыми интервалами.

Рис. 2.7

Плотность распределения интервала между любыми событиями, может быть представлена в виде:

f (t)=d(t-m_t), (2.59)

где d(t) – известная дельта-функция.

Так как интервал между соседними точками строго постоянен и равен m_t, то очевидно математическое ожидание этого интервала равно m_t, а D_t = 0.

Найдем закон распределения времени Q от случайной точки до наступления очередного события:

. (2.60)

Характеристическая функция интервала между соседними событиями в регулярном потоке будет иметь вид:

g (x)= e^-imtx. (2.61)

Регулярный поток событий сравнительно редко используется при решении прикладных задач. Это объясняется тем, что такой поток событий обладает очень большим (неограниченным) последействием, так как, зная лишь один момент наступления событий в регулярном потоке, можно восстановить всё прошлое этого потока и предсказать будущее.

Дата добавления: 2014-01-07