Минимизация дисперсии сигнала ошибки замкнутой системы

Рассмотрим линейную систему следующего вида:

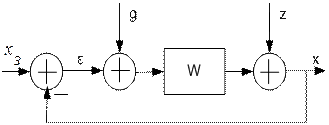
Рис. 5.22

На систему действуют случайные возмущения 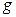и с известными спектральными плотностям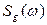и и . Задающее воздействие 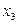также является случайным сигналом со спектральной плотностью 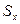. Пусть все три воздействия – центрированные сигналы. Тогда и сигнал ошибки 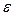тоже будет центрированным.

Если внешние воздействия не коррелированны между собой, то сигнал ошибки 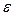, возникающий в системе, может рассматриваться как сумма трех независимых составляющих:

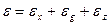(5.58)

Рис. 5.23

Составляющая обусловлена неточным воспроизведением задающего воздействия, а составляющие 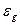и 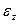- неполным подавлением возмущени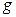й и . Соответственно дисперсия сигнала ошибки будет определяться как:

(5.59)

Дисперсия случайного сигнала согласно (5.57) зависит от амплитудной частотной характеристики 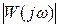, которая определяется на основе передаточной функции

Передаточные функци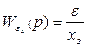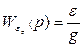и , и 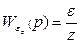могут быть вычислены по схемам:

Рис. 5.24

Рис. 5.25

Рис. 5.26

(5.60)

(5.61)

(5.62)

Каждая из дисперсий определяется по формулам:

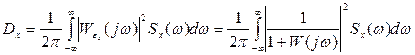(5.63)

(5.64)

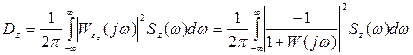(5.65)

При подстановке в формулы (5.63)-(5.65) конкретных значений и получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют следующий прием. Подынтегральное выражение представляют в типовой форме – в виде отношения двух полиномов от переменной :

, (5.66)

где

(5.67)

Полином всегда имеет степень ниже 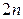и содержит только четные степени . Если в числителе окажутся нечетные степени, их можно отбросить.

В полиноме в виде сомножителя входит характеристическое уравнение замкнутой системы. Поэтому при приближении системы к границе устойчивости интеграл (5.66) резко возрастает.

Интегралы вида (5.66) для различных степеней вычислены заранее и приведены в справочниках по теории управления. Для степеней интегралы равны:

(5.68)

Представление интегралов (5.63)- (5.65) в форме (5.66) возможны практически для любой реальной системы, не содержащей запаздывание. Получив таким образом аналитическое значение дисперсии ошибки, получаем функцию от параметров системы:

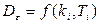, (5.69)

где 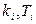- параметры системы. Минимизируя выражение (5.69) по параметрам 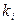и , можно определить их оптимальные значения.

Пример

Определить оптимальное значение передаточного коэффициента с передаточной функцией .

На входе системы действует задающее воздействие 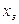со спектральной плотностью .

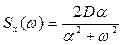На систему действует возмущение 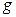в виде белого шума с ограниченной спектральной плотностью для .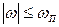

Внешнее воздействие отсутствует.

Таким образом, дисперсия сигнала ошибки определяется:

Дисперсия, обусловленная неточным воспроизведением задающего воздействия, имеет вид:

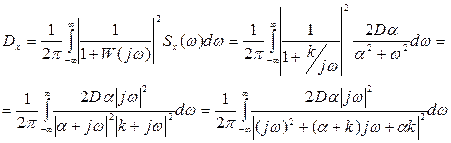
Сравнивая выражение с типовой формой записи интеграла (66), можно получить:

Окончательно дисперсия имеет вид:

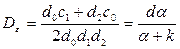
нетрудно заметить, что чем больше коэффициент 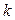, тем меньше дисперсия , то есть тем точнее система воспроизводит на выходе задающее воздействие.

Дисперсия, обусловленная неполной компенсацией возмущения

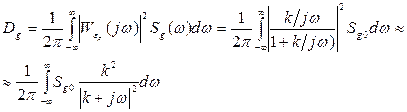
У этого интеграла:

Окончательно дисперсия имеет вид:

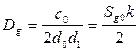
Чем больше коэффициент 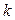, тем больше ошибка из-за прохождения возмущения 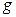на выход системы.

Суммарная дисперсия сигнала ошибки:

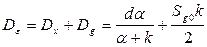
Оптимальное значение коэффициента усиления 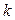найдем из условия:

Откуда имеем:

оптимальное значение передаточного коэффициента системы зависит от соотношения уровней задающего и возмущающего воздействий.

Дата добавления: 2014-01-07