Системы, оптимальные по быстродействию

Управление, оптимальное по быстродействию, может быть осуществлено как в разомкнутых, так и в замкнутых системах.

Разомкнутые системы (рис. 6.3, а) применяются в тех случаях, когда возмущающие воздействия на объект либо отсутствуют, либо заранее известны (в виде функций времени). Разомкнутая система содержит программное устройство ПУ, которое после пусковой команды выдает заранее рассчитанную программу изменения управляющего воздействия. Причем в устройство может быть заложено несколько программ, оптимальных для различных начальных, состояний объекта.

В замкнутых системах (рис. 6.3, б) оптимальное по быстродействию управление осуществляется при помощи включенного в контур вычислительного устройства ВУ. В это устройство вводятся текущие значения фазовых координат объекта, благодаря чему обеспечивается управление, оптимальное при различных внешних воздействиях.

Рис. 6.3. Функциональные схемы оптимальных по быстродействию систем

Для построения оптимальной замкнутой системы необходимо определить алгоритм функционирования вычислительного устройства в виде зависимости у(х). Общего метода отыскания этого алгоритма не существует. Ниже будет дан пример решения задачи для частного случая.

Синтез оптимальной разомкнутой системы заключается в расчете оптимальной программы у(t). Наиболее общим методом решения этой задачи является принцип максимума, разработанный группой советских математиков под руководством акад. Л. С. Понтрягина.

Рассмотрим вначале сущность принципа максимума Понтрягина применительно к общей задаче оптимального управления (6.7) — (6.10), а затем используем его для синтеза системы, оптимальной по быстродействию.

Введем дополнительную фазовую координату х₀ (t), характеризующую текущее значение функционала (6.4):

(6.11)

(С целью упрощения изложения здесь и далее принято х₃ (t) = 0 и z (t) = 0).

Для этой координаты справедливо следующее дифференциальное уравнение:

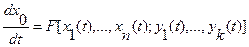(6.12)

Вводя для функции F обозначение f ₀ и присоединяя уравнение (6.12) к системе (6.7), можно записать новую систему уравнений:

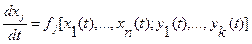(6.13)

(j=0; 1;...; n)

Теперь задача оптимальною управления сводится к отысканию такого решения системы (6.13), при котором дополнительная координата х₀(t) в конце движения принимает наименьшее значение х₀ (t_n)= Q, а остальные переменные удовлетворяют граничным условиям (6.10).

Дли решения задачи, вводятся вспомогательные функции , которые удовлетворяют системе уравнений

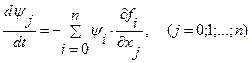(6.14)

Функции 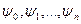можно рассматривать как компоненты некоторого вектора ψ, который равен (по модулю) градиенту функционала Q в (n+1)-мерном фазовом пространстве и направлен в противоположную сторону. Производные фазовых координат также можно считать компонентами вектора f, который характеризует скорость движения изображающей точки в фазовом пространстве.

Согласно принципу максимума оптимальными являются такие управляющие воздействия y₁(t), y₂(t),..., y_k(t), при которых в каждый момент времени скалярное произведение векторов ψ и f максимально, т. е.

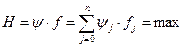, (6.15)

причем максимальное значение Н равно нулю.

Управляющие воздействия, максимизирующие функцию H, должны, очевидно, удовлетворять следующей системе уравнений:

. (6.16)

Но в этой системе k уравнений содержится (2 n + k + 2) неизвестных: (n + 1) функций x_j (t), (n +1) функций ψ_j(t) и k функций y_l (t). Поэтому для отыскания функций y_l (t) необходимо еще учесть (n + 1) уравнений объекта (6.13) и (n + 1) вспомогательных уравнений (6.14).

Так как функции f_j не зависят от функций ψ_j, то

(6.17)

Учитывая соотношения (6.17), можно уравнения объекта (6.13) и вспомогательные уравнения (6.14) объединить в удобной канонической форме:

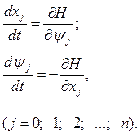(6.18)

Уравнения вида (6.18) называют системой Гамильтона, а функцию Н — гамильтонианом.

Если целью оптимизации является максимальное быстродействие системы, то, как известно из 6.1, f₀ = F =1 функция H принимает вид

(6.19)

Применим принцип максимума к линейному объекту n -го порядка с одним ограниченным по модулю управляющим воздействием y. Для этого представим уравнение объекта в виде системы

(6.20)

Управляющее воздействие согласно условию имеет ограничение

(6.21)

Вспомогательные уравнения (6.14) в данном случае имеют вид

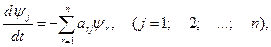(6.22)

а гамильтониан (13.19)

(6.23)

Очевидно, что гамильтониан (6.23) принимает максимальные значения только при

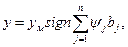(6.24)

а это означает, что управляющее воздействие у в любой момент времени должно принимать только предельные значения +у_м или – у_м.

Оценим теперь число необходимых переключений управляющего воздействия у_м.

Если все корни характеристического уравнения объекта действительны, то такими же будут и корни характеристического уравнения, соответствующего вспомогательным уравнениям (6.22), и решения системы (6.22) будут иметь вид

(6.25)

При этом управляющее воздействие (13.24) изменяется по закону

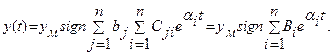(13.26)

Сумма n экспонент, стоящая под знаком sign, может перейти через нуль не более (n -1) раз. Следовательно, оптимальное управляющее воздействие представляет собой кусочно-постоянную функцию (рис.13.4), принимающую только предельные значения ± y_м и имеющую не более n интервалов постоянства.

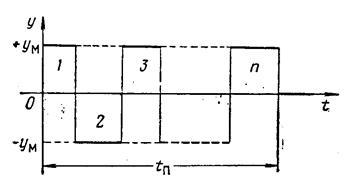
Рис. 6.4. Управляющее воздействие в системе, оптимальной по быстродействию.

Этот принцип, получивший наименование «теоремы об n интервалах», впервые был сформулирован одним из основоположников отечественной школы теории управления проф. А. А. Фельдбаумом.

Теорема об n интервалах справедлива только для линейных объектов с одним ограничением и при нулевых начальных условиях. При ненулевых условиях число интервалов может быть меньше n. Если ограничение наложено не только на управляющее воздействие, но и на некоторые фазовые координаты, то число интервалов больше n. Причем на каждом из интервалов на предельном уровне находится лишь одна координата.

При наличии у объекта комплексных корней число интервалов может быть сколь угодно большим.

Проиллюстрируем применение принципа максимума на простейшем примере. Пусть объект управления описывается дифференциальным уравнением

(6.27)

Требуется найти законы управления у (t) и у (х), обеспечивающие максимальное быстродействие системы при переходе ее из произвольного начального состояния в равновесное состояние (х = 0, dx/dt = 0). На управляющее воздействие наложено ограничение (6.21), которое в данном случае эквивалентно ограничению второй производной:

, (6.28)

где

Отметим, что уравнение (6.27) соответствует широкому классу механических объектов, в которых происходят процессы перемещения больших масс без трения. Применительно к таким объектам переменная х означает линейное или угловое перемещение, а переменные х’ и х" — соответственно линейные (угловые) скорости и ускорении. Управляющим воздействием y является сила или момент, создаваемые приводом. Коэффициент k ₀ в таком случае равен единице, деленной на массу или момент инерции. Электрическая инерционность привода и силы сопротивления при этом не учтены.

Найдем вначале оптимальную программу у (t) разомкнутой системы.

Обозначая х = x₁ и dx/dt = х₂, уравнение объекта можно записать в форме (6.13):

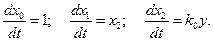(6.29)

Гамильтониан (6.19) в данном случае равен

(6.30)

Он линейно зависит от переменной у и, следовательно, принимает свои наибольшие значения лишь тогда, когда у (t) = + у_м или у (t) = — у_м. Очевидно, что при ψ ₂ (t) > 0 управляющее воздействие должно быть равно +у_м, а при ψ ₂ (t) < 0 — значению — у_м. Такой закон управления можно записать при помощи знака sign:

(6.31)

Вспомогательные функции ψ ₀, ψ ₁, ψ ₂ можно найти по уравнениям (6.14), (6.18) или (6.22):

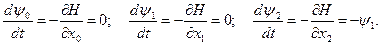(6.32)

Решения этих уравнений будут:

(6.33)

Отсюда окончательно закон оптимального управления

(6.34)

Так как функция меняет знак не более одного раза, то управляющее воздействие (6.34) представляет собой кусочно-постоянную функцию, имеющую не более двух интервалов постоянства и принимающую только предельные значения +у_м и — у_м.

Момент переключения управляющего воздействия зависит от начальных условий x₁₀ и x₂₀. В наиболее распространенном частном случае, когда х₂₀ = 0, оба интервала равны друг другу (рис. 6.5, б) и в сумме составляют

(6.35)

В более общих случаях определение моментов переключения представляет собой довольно громоздкую вычислительную задачу.

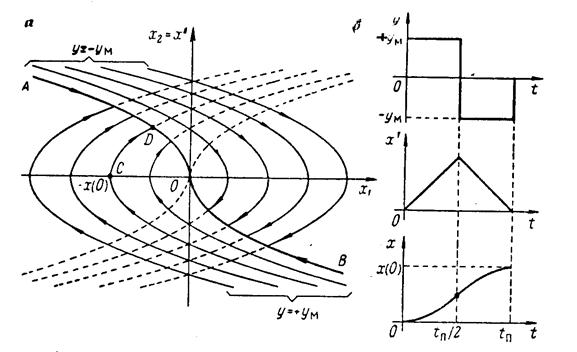
Рис. 6.5. Фазовый портрет (в) и переходные процессы (б) оптимальной системы второго порядка

Полученный закон управления вытекает также из следующих физических соображений. Наибыстрейшее перемещение объекта на величину x₁₀ = х (0) произойдет, если вначале осуществлять разгон с максимально допустимым ускорением +х"_м, а затем после достижения середины пути начать торможение с максимально допустимым замедлением — х"_м (отрицательным ускорением). При этом (см. рис. 13.5, б) скорость перемещения х' на каждом интервале изменяется по линейному закону, а кривая х (t) состоит из ветвей двух парабол.

Синтез управляющего устройства, реализующего максимальное быстродействие в замкнутой системе, осуществим с помощью фазовой плоскости.

Исключая из уравнений (6.29) величину dt, получаем дифференциальное уравнение

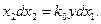(6.36)

Интегрируя выражение (6.36), находим уравнения фазовых траекторий:

при у= + у_м

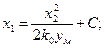(6.37)

при y= — у_м

(6.38)

На фазовой плоскости (рис. 6.5, а) уравнению (6.37) соответствует семейство парабол с ветвями, расположенными справа от вершины, а уравнению (6.38) — семейство парабол с ветвями, расположенными слева от вершины. Смещение вершин парабол по оси x₁ определяется постоянными интегрирования С, которые зависят от начальных условий x ₁₀ и x ₂₀.

Так как по условию задачи процесс должен закончиться в начале координат, то на последнем этапе процесса изображающая точка будет двигаться обязательно по одной из двух парабол, проходящих через начало координат. Причем, согласно общему свойству фазовых траекторий движение к началу координат может происходить лишь по одной ветви каждой параболы: при x ₂ >0 — по ветви АО, расположенной во втором квадранте, и при х₂ < 0 — по ветви ВО, расположенной в четвертом квадранте.

Эти две ветви, принадлежащие параболам из разных семейств, можно описать одним общим уравнением

(6.39)

Если в начальном состоянии изображающая точка расположена выше линии АОВ, то под воздействием управления у = — y_м система будет двигаться к завершающему участку ВО по траекториям (6.38). Если же точка расположена ниже линии АОВ, то у = +у_м, и движение происходит по траектории (6.37) до их пересечения с ветвью АО.

В обоих случаях при попадании изображающей точки на линию АОВ происходит переключение управляющего воздействия с одного предельного значения на другое. Таким образом, линия АОВ является линией переключения. Переходным процессам, показанным на рис. 6.5, б, соответствует, конкретная фазовая, траектория CDO.

Теперь, зная уравнение линии переключения, можно синтезировать оптимальное управляющее устройство (рис. 6.6). Оно состоит из двухпозиционного исполнительного устройства ИУ и вычислительного устройства ВУ.

Исполнительное устройство имеет ограниченную выходную величину и описывается функцией

(6.40)

Вычислительное устройство реализует так называемую переключающую функцию

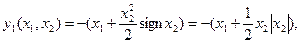(6.41)

которая на линии переключения (6.39) равна нулю. В точках фазовой плоскости, расположенных правее линии переключения, функция y ₁ <0, а управляющее воздействие согласно (6.40) равно у = — у_м. В точках, расположенных левее линии переключения, функция y ₁ > 0, а у = +у_м.

Рис. 6.6. Алгоритмическая схема оптимальной системы второго порядка

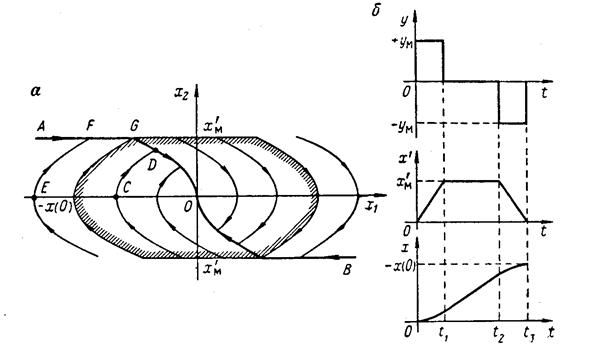
Рис. 6.7. Фазовый портрет (а) и переходные процессы (б) оптимальной системы с ограниченными ускорением и скоростью

Если у рассматриваемого объекта второго порядка ограничить не только ускорение, но и скорость х' = х₂, то на фазовом портрете оптимальной системы (рис. 6.7, а) появится замкнутая область, за пределами которой действует ограничение х' <x'_м. При достаточно большом начальном отклонении х (0) объект после разгона до предельной скорости х'_м будет некоторое время двигаться с этой постоянной скоростью, а затем начнется торможение с предельным замедлением х"_м (рис. 6.7, б). Такому процессу соответствует фазовая траектория EFGO. Оптимальные процессы с ограниченными значениями скорости и ускорения используют при управлении шахтными подъемными установками.

Дата добавления: 2014-01-07