Растворы слабых кислот и оснований

Диссоциация многих электролитов протекает не полностью. Отношение числа диссоциированных молекул к общему числу молекул электролита в растворе называют степенью диссоциации. Для одноосновной кислоты, диссоциирующей по уравнению:

НА Û Н⁺ + А^-, где А - кислотный остаток, (14)

степень диссоциации a равна:

a = [Н⁺] / С,(15)

где С - концентрация кислоты в моль/л или в моль/кг.

Многоосновные кислоты диссоциируют ступенчато, например:

Н₃РО₄ Û Н₂РО₄^- + Н ⁺ (1-ая ступень);

Н₂РО₄^- Û НРО₄^2- + Н⁺ (2-ая ступень);

НРО₄^2- Û РО₄^3- + Н⁺ (3-я ступень).

Обычно константа диссоциации по второй ступени приближенно в 10⁴-10⁵ раз ниже, чем по первой. По третьей ступени константа диссоциации еще во столько же раз ниже. Поэтому при расчетах рН в растворах многоосновных слабых кислот обычно учитывают только первую ступень диссоциации, пренебрегая второй и третьей ступенями. Таким образом, уравнение (14) приближенно описывает диссоциацию и многоосновных кислот.

Диссоциация слабых электролитов - равновесный процесс. Для его количественного описания используют константу равновесия, называемую константой диссоциации:

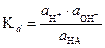(16)

Константу диссоциации находят в справочнике или рассчитывают по термодинамическим данным:

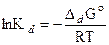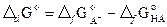, где (17)

Энергии Гиббса образования A^- и HA в водном растворе при 298 К находят в справочнике. Константы диссоциации при других температурах рассчитывают по уравнению изобары реакции в интегральной форме:

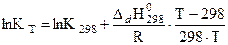(18)

Значение константы диссоциации используют для расчета рН раствора.

В рамках теории Дебая и Хюккеля по уравнению (6) получаем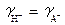и 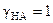. Согласно уравнению (14) [Н⁺] = [А^-]. Следовательно, a _H + = a _A -. Равновесная концентрация недиссоциированной кислоты равна разности между общей концентрацией и концентрацией образовавшихся ионов. С учетом формулы (15) получаем:

[НА] = С - [Н⁺] = С - aС = С(1 - a).

Так как в растворах слабых электролитов при умеренных разбавлениях a<< 1, то [НА] @ С. Преобразуем формулу (16):

отсюда 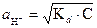(19)

После логарифмирования уравнения (19) получаем:

(20)

Для растворов слабых оснований можно вывести аналогичные формулы:

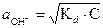(21)

, ( 22 )

где С - концентрация слабого основания, моль/кг.

По значению константы диссоциации можно рассчитать степень диссоциации слабого электролита. Из формулы (19) следует:

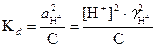(23)

Домножив в (23) числитель и знаменатель дроби на С, с учетом формулы (15) получаем: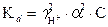. Отсюда следует:

(24)

Если в растворе нет посторонних солей, то ионная сила слабого электролита близка к нулю, и g_Н+@1 согласно уравнению (6). В отсутствие солевого фона (24) переходит в известную формулу Оствальда:

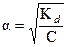(25)

Словесная формулировка закона Оствальда: Степень электролитической диссоциации обратно пропорциональна квадратному корню из концентрации раствора.

Дата добавления: 2014-01-07