
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Смешанное произведение векторов
|
|
|
|
Определение 1.7.1. Пусть  – упорядоченная тройка произвольных векторов. Смешанным произведением тройки векторов
– упорядоченная тройка произвольных векторов. Смешанным произведением тройки векторов  называется число
называется число  Смешанное произведениеобозначается
Смешанное произведениеобозначается 
Пусть  – некомпланарные векторы. Отложим их от некоторой точки
– некомпланарные векторы. Отложим их от некоторой точки 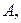 получим точки соответственно
получим точки соответственно 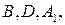 не лежащие в одной плоскости с точкой
не лежащие в одной плоскости с точкой  Следовательно, отрезки
Следовательно, отрезки 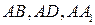 можно считать тремя ребрами параллелепипеда
можно считать тремя ребрами параллелепипеда 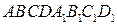 , выходящими из одной вершины
, выходящими из одной вершины  (рис. 7.1).
(рис. 7.1).

Рис. 7.1
Этот параллелепипед будем называть параллелепипедом, построенным на векторах 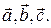 Обозначим
Обозначим 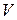 число, выражающее объем этого параллелепипеда. Введенные обозначения будем использовать в следующей теореме, выражающей геометрический смысл смешанного произведения.
число, выражающее объем этого параллелепипеда. Введенные обозначения будем использовать в следующей теореме, выражающей геометрический смысл смешанного произведения.
Теорема 6.1. Пусть  – некомпланарные векторы. Тогда
– некомпланарные векторы. Тогда
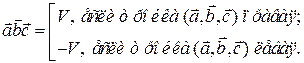
Доказательство. Пусть  – прямая, проходящая через точку
– прямая, проходящая через точку  перпендикулярно основанию
перпендикулярно основанию  параллелепипеда,
параллелепипеда,  – единичный вектор прямой
– единичный вектор прямой 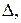 выбранный так, что тройка
выбранный так, что тройка 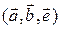 – правая (рис.7.2, 7.3). Тогда
– правая (рис.7.2, 7.3). Тогда 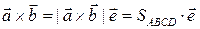 и
и 
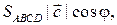 где
где 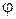 – величина угла между векторами
– величина угла между векторами 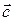 и
и 
Если тройка  как и
как и  правая, то векторы
правая, то векторы  и
и 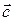 лежат в одном полупространстве относительно плоскости основания
лежат в одном полупространстве относительно плоскости основания  и
и  (рис. 7.2). В этом случае
(рис. 7.2). В этом случае 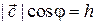 – длина высоты параллелепипеда, проведенной к основанию
– длина высоты параллелепипеда, проведенной к основанию  и, следовательно,
и, следовательно, 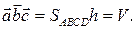


Рис. 7.2 Рис. 7.3
Если же тройка  – левая, то векторы
– левая, то векторы  и
и 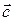 лежат в различных полупространствах относительно плоскости основания
лежат в различных полупространствах относительно плоскости основания  и
и  (рис. 7.3). В этом случае
(рис. 7.3). В этом случае  и, следовательно,
и, следовательно, 

Следствие 1.6.1. Векторы  компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда  Другими словами, равенство нулю смешанного произведения трех векторов – критерий их компланарности.
Другими словами, равенство нулю смешанного произведения трех векторов – критерий их компланарности.
Доказательство. Необходимость. Пусть векторы  компланарны. Если
компланарны. Если 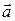 и
и  коллинеарны то
коллинеарны то  и, следовательно,
и, следовательно,  Если же
Если же 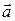 и
и  не коллинеарны, то
не коллинеарны, то  поэтому
поэтому  Следовательно
Следовательно 
Достаточность. Пусть  Допустим, что
Допустим, что  не компланарны. Тогда на этих векторах можно построить параллелепипед, объем которого равен
не компланарны. Тогда на этих векторах можно построить параллелепипед, объем которого равен 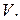 По теореме 1.6.1
По теореме 1.6.1  Получили противоречие с условием достаточности. Следовательно, векторы
Получили противоречие с условием достаточности. Следовательно, векторы  компланарны.
компланарны.
Следствие 1.6.2. Для любых трех векторов  верны равенства:
верны равенства:
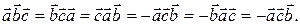
Доказательство. Если векторы  компланарны, то, согласно следствию 6.1, все шесть рассматриваемых чисел равны нулю. Если векторы
компланарны, то, согласно следствию 6.1, все шесть рассматриваемых чисел равны нулю. Если векторы  не компланарны, то на этих векторах можно построить параллелепипед, объем которого равен
не компланарны, то на этих векторах можно построить параллелепипед, объем которого равен  и, согласно теореме 1.6.1, все шесть рассматриваемых чисел по абсолютной величине равны
и, согласно теореме 1.6.1, все шесть рассматриваемых чисел по абсолютной величине равны 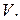 Знаки этих чисел зависят от ориентации соответствующей тройки. В § 1.4 отмечалось, что упорядоченные тройки
Знаки этих чисел зависят от ориентации соответствующей тройки. В § 1.4 отмечалось, что упорядоченные тройки  имеют одинаковую ориентацию, а тройки
имеют одинаковую ориентацию, а тройки  – противоположную. Следовательно, числа
– противоположную. Следовательно, числа 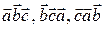 равны и противоположны числам
равны и противоположны числам 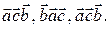
Пусть векторы 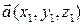 ,
, 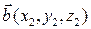 ,
,  заданы своими координатами в некотором правом ортонормированном базисе
заданы своими координатами в некотором правом ортонормированном базисе 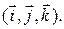 Тогда, согласно формуле (4) из § 1.5, вектор
Тогда, согласно формуле (4) из § 1.5, вектор  имеет следующие координаты:
имеет следующие координаты:
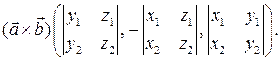
Следовательно,

Так как, согласно следствию 6.2, 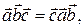 то окончательно получаем следующую формулу для вычисления смешанного произведения векторов по их координатам:
то окончательно получаем следующую формулу для вычисления смешанного произведения векторов по их координатам:
 (1)
(1)
Согласно следствию 1.6.2, критерием компланарности векторов  является равенство нулю определителя (1), составленного из координат векторов в ортонормированном базисе. Далее в § 1.8 будет показано, что это же верно для произвольного базиса (утверждение 1.8.2).
является равенство нулю определителя (1), составленного из координат векторов в ортонормированном базисе. Далее в § 1.8 будет показано, что это же верно для произвольного базиса (утверждение 1.8.2).
[1] Как показывают приведенные ниже рассуждения, доказываемая формула справедлива для поворота не только на но и на любой другой угол.
[2] См. [ ], §.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 717; Нарушение авторских прав?; Мы поможем в написании вашей работы!