Метод комплексных амплитуд

Способы представления гармонических колебаний

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы, см. рис. 2.1); вращающимися векторами (векторные диаграммы); комплексными числами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

Временное представление наглядно, однако требует проведения громоздких тригонометрических преобразований.

Наиболее распространенным является представление гармонических колебаний с помощью комплексных чисел. Это представление лежит в основе символического метода расчета цепей – метода комплексных амплитуд.

Суть метода состоит в том, что исходной гармонической функции, называемой оригиналом, ставится в соответствие комплексная функция, называемой изображением. Все операции при решении задач проводят над изображениями, которые оказываются более простыми, т.к. система ДУ преобразуется в систему алгебраических уравнений, в которых переменными являются комплексные амплитуды напряжений или токов.

После решения системы уравнений производят обратное преобразование: от искомой комплексной переменной (изображения) переходят к искомой функции времени (оригиналу).

В основе преобразования гармонической функции времени в комплексное число лежит формула Эйлера 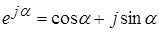, (2.4)

где – мнимая единица.

Умножим формулу (2.4) на амплитуду гармонической функции, например, напряжения U_m, а аргумент α в формуле (2.4) приравняем к полной фазе гармонического напряжения (2.1) α = θ (t) = (ω t + φ₀). Тогда получится комплексная функция, которую принято называть мгновенным комплексным значением гармонической функции напряжения и обозначать подчеркиванием знака функции – u(t):

(2.5)

Функция (2.5) является изображением функции (2.1) – оригинала. Связь между оригиналом и изображением формально записывается так

u(t) ÷ u(t) (2.6)

Аналогично можно записать оригинал и изображение мгновенного значения тока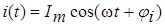

. (2.7)

Выражения комплексных напряжения(2.5) и тока (2.7) записаны в двух формах – показательной и тригонометрической.

Мгновенное значение напряжения является реальной частью мгновенного комплексного значения, т.е.

u(t)= Re [ u(t) ] = U_m cos(ω t + φ_u) = a_u, (2.8)

где Re – сокращенное обозначение слова Realis (действительный, вещественный). Если мгновенное значение напряжения задается в форме синусоиды, например u(t) = U_m sin(ω t + φ_u), то это значение является мнимой частью комплексной функции и обозначается так:

u(t) = Im [ u(t) ] = U_m sin(ω t + φ_u) = b_u, (2.9)

где Im = сокращенное обозначение слова Imaginarins (мнимый).

Следовательно, мгновенное комплексное значение напряжение можно записать в алгебраической форме

u(t) = a_u + jb_u. (2.10)

Дата добавления: 2014-01-07