Модальное управление

Лекция 6

Еще один подход к синтезу многомерных систем регулирования дает теория модального управления. Эта теория существенным образом основывается на линейности рассматриваемых моделей; с ее помощью можно устанавливать желаемые значения собственных чисел замкнутой системы. Разберем основные положения модального управления на примере стандартной линейной системы в пространстве состояний

(1) (2)

Будем предполагать, что в уравнениях (1), (2) размерности векторов управления и выхода совпадают и равны размерности пространства состояний, что А, В, С — постоянные матрицы и что все собственные числа матрицы А действительны и различны. Эти предположения не являются ограничивающими [12], они служат лишь для упрощения последующих выводов. Будем строить управление в виде пропорциональной обратной связи по выходам

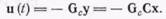(103)

, Напомним теперь определение собственных чисел и векторов. Если— диагональная матрица собственных чисел квадратной матрицы

(104)

то справедливы следующие соотношения:

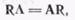(105)

(106)

где R и L—матрицы нормированных собственных векторов (левых и правых) матрицы А, т. е. R и L определяются как решения векторных уравнений:

(107)

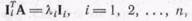(108)

а собственные числа Я,- являются решениями характеристического уравнения

(109)

Все векторы I,- и г* нормируются так, чтобы они были ортонормальны:

(110)

или же в матричной форме:

(111)

где (112)

Умножая (105) слева на L, а (106)—на R и используя (11), получим следующие выражения:

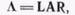(113)

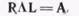. (114)

Подставляя (103) и (114) в (3.2.1),найдем

(115)

Если теперь взять матрицу Gc так, чтобы выполнялось равенство

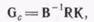(116)

где диагональная матрица К представляет собой матричный коэффициент усиления в цепи обратной связи

(117)

а матрицу наблюдения С равной L, то получим уравнение (115) в преобразованном виде

(118)

Сделав замену переменных

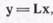(119)

получим уравнение относительно у

(120)

Поскольку диагональная матрица, система (120) разлагается на независимые уравнения первого порядка, решениями которых являются функции

(121)

Возвращаясь к прежним переменным, получим решение в пространстве состояний

(122)

Здесь коэффициенты а,- определяются начальными условиями. Изменяя k_i, можно как угодно менять собственные числа замкнутой системы, при этом между разными выходами нет взаимосвязей, т. е. изменение коэффициента усиления k, влияет только на i-моду. Это означает, что имеется возможность управлять модами замкнутой системы, причем перекрестные связи между координатами состояния не сказываются на выходе. В качестве недостатков представленной методики следует отметить, что используются только пропорциональные регуляторы, матрица С должна совпадать с L и, как показывает практика, трудна настройка системы. Блок-схема системы приведена на рис. 1.

Если размерность вектора управления т меньше размерности вектора состояния, то модальное управление может быть применено к первым т собственным векторам матрицы А

Рис.1. Блок-схема системы модального регулирования

Дата добавления: 2014-01-07