Третий случай соответствует эллипсоидальным изоэнергетическим поверхностям

Если изоэнергетические поверхности имеют вид эллипсоидов (рис.1.54, 1.55), тогда:

(2.16)

Где 1/m₁, 1/m₂ и 1/m₃ – диагональные компоненты тензора обратной эффективной массы. Уравнение эллипсоида в канонической форме:

(2.17)

где полуоси эллипсоида

(2.18)

Объем одного эллипсоида с полуосями а₁, a₂, a₃ равен

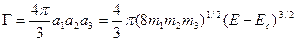, (2.19)

а объем одного тонкого слоя между двумя эллипсоидальными изоэнергетическими поверхностями

(2.20)

Подставляя dГ в выражение для dN и учитывая, что минимумов энергии может быть М, получим

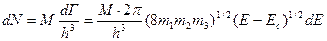(2.21)

или

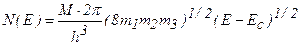. (2.22)

Таким образом, плотность состояний пропорциональна (Е—Е_с)^1/2 и (m₁m₂m₃)^1/2, где m₁,m₂,m₃ — компоненты тензора эффективной массы (в главных осях). При малых m_i N(Е) будет малой величиной.

Если положить

, (2.23)

где 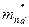— носит название эффективной массы плотности квантовых состояний для электронов, то в общем случае, с учетом двух ориентаций спина:

(2.24)

что совершенно аналогично (2.12) для случая изотропной массы с одним минимумом. То есть, эллипсоидальную поверхность равной энергии зоны проводимости можно заменить сферой, если ввести эффективную массу плотности состояний для электронов, которая вычисляется по формуле (2.23).

Выражение (2.24) является наиболее общим, поскольку из него вытекают (2.12), (2.15) как частные случаи. Необходимо только помнить, что зависимость N(Е) от энергии вида 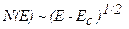справедлива до тех пор, пока энергия являете квадратичной функ­цией квазиимпульса, другими словами, выражение (2.24) справедли­во только для состояний вблизи минимума энергии, т. е. у дна зоны проводимости.

Найдем выражение для плотности квантовых состояний у потолка валентной энергетической зоны, где энергия также является квадратичной функцией энергии. Если максимумы энергии находятся в точках k₀ зоны Бриллюэна, а их число равно М, то Е(k) (для каждого максимума) можно представить в общем виде:

(2.25)

Учитывая, что тензор эффективной массы электронов в максимуме энергии отрицателен, введем вместо него тензор эффективной массы дырок 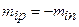. Тогда следует

(2.26)

или

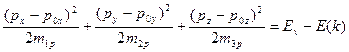, (2.27)

где 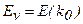- в данном случае - энергия потолка валентной зоны. Опуская совершенно очевидные выкладки, найдем, что выражение для плотности квантовый состояний (с учетом ориентации спина) у потолка зоны имеет вид:

, (2.28)

где через , обозначена эффективная масса дырок для плотности. состояний:

, (2.29)

Дата добавления: 2014-01-07