
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функции распределения частиц. Функция Ферми-Дирака
|
|
|
|
Функцией распределения в статистической теории принято называть функцию, которая в условиях термодинамического равновесия при заданной температуре Т пропорциональна вероятности того, что некоторая частица занимает определенный энергетический уровень Е.
Вид функции распределения зависит от возможного количества частиц в данном разрешенном энергетическом состоянии и от того, являются ли данные частицы различимыми. Различимость – это свойство частиц изменять физические характеристики твердого тела при перестановке частиц местами.
В классической физике частицы считаются различимыми и могут неограниченно заполнять одно и то же энергетическое состояние. Распределение частиц газа по энергиям описывается с помощью функции распределения Максвелла - Больцмана:
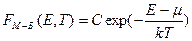 ;
; 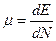 (2.32)
(2.32)
где μ – химический потенциал, выражающий изменение свободной энергии системы при изменении числа частиц в системе на одну при постоянной температуре и постоянном объеме системы: 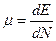 (фактически – работа выхода); С – постоянная, которая находится из условия, что сумма частиц на всех уровнях системы равна некоторому заданному и неизменному числу N. Название химический потенциал, а не какой–либо другой, подчеркивает лишь то обстоятельство, что рассматриваемые частицы способны двигаться по законам механики.
(фактически – работа выхода); С – постоянная, которая находится из условия, что сумма частиц на всех уровнях системы равна некоторому заданному и неизменному числу N. Название химический потенциал, а не какой–либо другой, подчеркивает лишь то обстоятельство, что рассматриваемые частицы способны двигаться по законам механики.
В отличие от классических представлений в квантовой механике микрочастицы являются неразличимыми. Микрочастицы подразделяются на 2 группы: бозоны и фермионы. Бозоны могут неограниченно заполнять одно и то же энергетическое состояние, причем тем легче, чем больше их в этом состоянии находится. Фермионы подчиняются запрету Паули. Это значит, что одно квантовое состояние может быть занято не более чем одним фермионом.
К бозонам относятся: фотоны, фононы, пионы, а к фермионам - электроны, протоны, нейтроны.
Бозоны подчиняются статистике Бозе-Эйнштейна
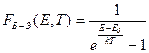 (2.33)
(2.33)
В условиях равновесия бозоны имеют минимум свободной энергии, поэтому химический потенциал бозонов равен нулю. Отсюда следует
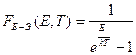 (2.33А)
(2.33А)
Распределение фермионов по энергетическим уровням описывается с помощью функции Ферми-Дирака:
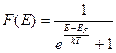 (2.34)
(2.34)
где k – постоянная Больцмана, Т – температура, EF – энергия Ферми или электрохимический потенциал, т.е. работа, которую необходимо затратить для изменения числа частиц на одну единицу. В случае, когда частицами, составляющими статистическую систему, являются электроны, которые помимо массы обладают еще и электрическим зарядом, изменение энергии возможно за счет изменения заряда. Электрохимический потенциал, который представляет собой алгебраическую сумму химического и электростатического потенциалов, то есть равен (EF=μ-qj), где j - электростатический потенциал, и отражает это. Обычно его отождествляют с уровнем (энергией) Ферми. Можно показать, что в условиях термодинамического равновесия энергия Ферми оказывается постоянной в любой системе контактирующих тел. Поэтому необходимым условием равновесия системы можно считать постоянство уровня Ферми.
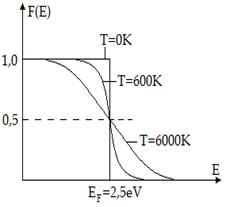
Характерно, что вид функции Ферми-Дирака не зависит от свойств системы, а зависит только от температуры. Конкретные свойства системы отражаются лишь на положении уровня Ферми. Графическое изображение функции распределения Ферми-Дирака представлено на рис. 2.4.
Основные свойства функции Ферми-Дирака.
1. 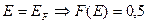 , т.е. уровень Ферми занят с вероятностью 0,5 (всегда!).
, т.е. уровень Ферми занят с вероятностью 0,5 (всегда!).
То есть уровень Ферми есть энергетический уровень, вероятность заполнения которого при температуре, отличной от абсолютного нуля равна 0.5.
2. 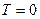 К. Тогда:
К. Тогда: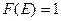 для
для 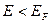 и
и 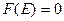 для
для 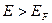 ,
,
т.е. при температуре 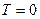 К все разрешенные состояния ниже уровня Ферми заняты, а все выше него – полностью свободны. Это отличается от случая классических частиц, когда при
К все разрешенные состояния ниже уровня Ферми заняты, а все выше него – полностью свободны. Это отличается от случая классических частиц, когда при 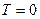 К все электроны имеют
К все электроны имеют 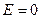 .
.
Следовательно, энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля.
3. Если энергия электронов значительно выше энергии Ферми, т.е. 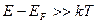 , тогда
, тогда
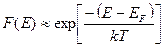 . (2.35)
. (2.35)
Формула (2.35) представляет собой классическое распределение Максвелла-Больцмана. Таким образом, функция Ферми-Дирака при больших энергиях переходит в распределение Максвелла-Больцмана.
4. Если энергия электрона ниже ЕF настолько, что 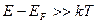 , тогда:
, тогда:
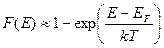 , (2.36)
, (2.36)
т.е. в области энергий, существенно меньших 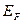 , разрешенные состояния заняты с вероятностью, близкой к 1.
, разрешенные состояния заняты с вероятностью, близкой к 1.
5. В области 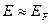 функция
функция 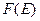 изменяется очень быстро от значений, близких к 1, до нуля. Скорость изменения зависит от
изменяется очень быстро от значений, близких к 1, до нуля. Скорость изменения зависит от 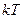 , и для температуры абсолютного нуля равна бесконечности (рис.2.4 в).
, и для температуры абсолютного нуля равна бесконечности (рис.2.4 в).
Функция распределения Ферми-Дирака (2.34) характеризует вероятность заполнения данного состояния электроном. Вероятность того, что в состоянии с энергией Е электрон отсутствует, т.е. оно занято дыркой, будет равна:
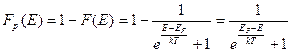 (2.37)
(2.37)
Следовательно, функция распределения для дырок аналогична функции распределения для электронов, если отсчитывать энергию дырок от уровня Ферми в противоположную сторону по сравнению с направлением отсчета энергии для электрона.
 (а)
(а)
|  (б) (б)
|
 (в) (в)
| |
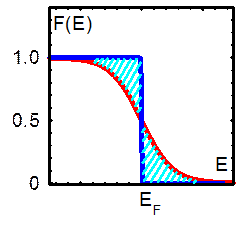
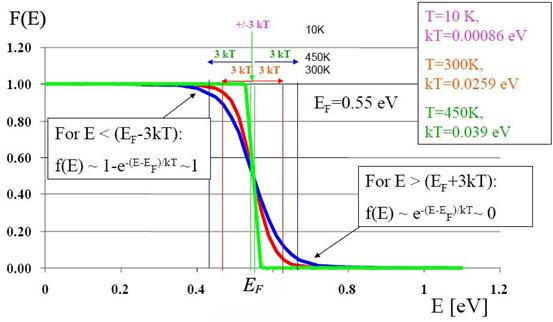
 Рис. 2.4. Распределение Ферми-Дирака. Рис. 2.4. Распределение Ферми-Дирака.
|

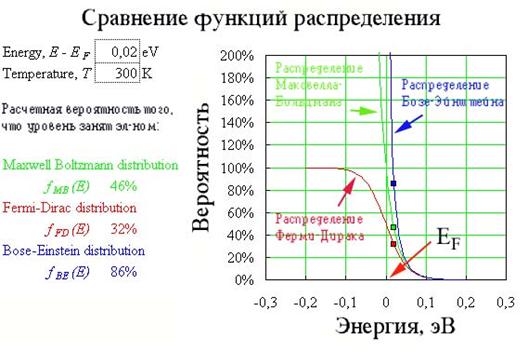
При Т >0 часть электронов за счет теплового движения смогут перейти в состояние с E > EF. Число частиц, перешедших на более высокие уровни, равно количеству образовавшихся свободных состояний в области Е < EF. Это означает, что заштрихованные на рис. 2.4 (б) площади равны. Кроме этого, нетрудно заметить, что величина F(E) заметно отличается от 1 или 0 лишь в пределах нескольких (~3)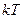 вблизи значения E=EF (рис.2.4 в). Из рисунка видно, что функция Ферми-Дирака испытывает сильное изменение от 0,953 до 0,047 при изменении
вблизи значения E=EF (рис.2.4 в). Из рисунка видно, что функция Ферми-Дирака испытывает сильное изменение от 0,953 до 0,047 при изменении 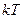 в интервале от –2 kT до +2 kT. В дополнение хорошо видно, что интервал энергии, определяющий резкое изменение F(E,Т), зависит от температуры: при Т ® 0 он стремится к нулю.
в интервале от –2 kT до +2 kT. В дополнение хорошо видно, что интервал энергии, определяющий резкое изменение F(E,Т), зависит от температуры: при Т ® 0 он стремится к нулю.
Полупроводники, у которых распределение свободных носителей заряда по энергетическим состояниям описывается функцией Ферми-Дирака, называются вырожденными. Вырожденными являются такие полупроводники, у которых уровень Ферми расположен вблизи края запрещенной зоны (как правило, на расстоянии менее нескольких kT).
Для электронов, находящихся в состояниях с энергией E-EF >>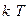 , выражение для F(E) принимает вид:
, выражение для F(E) принимает вид:
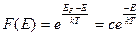 , (2.38)
, (2.38)
то есть совпадает с функцией распределения Максвелла-Больцмана для частиц, подчиняющихся классическим законам.
Если распределение носителей заряда по энергиям в полупроводнике подчиняются статистике Больцмана, то полупроводник называют невырожденными.
Невырожденными являются такие полупроводники, у которых уровень Ферми расположен внутри запрещенной зоны на расстоянии более нескольких kT от границы с разрешенной зоной.
2.3. Степень заполнения примесных уровней
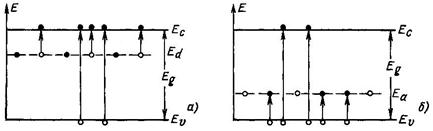
Рассмотрим полупроводник, содержащий донорную примесь в концентрации Nd. Донор, удерживающий электрон, электрически нейтрален. Это соответствует, например, случаю, когда один из узлов кристаллической решетки кремния занят атомом мышьяка. При этом пятый валентный электрон атома донорной примеси не принимает участия в ковалентной связи и ему соответствует энергетический уровень, расположенный ниже дна зоны проводимости на величину Еd (рис. 2.5 а).
Поскольку у донорной примеси имеется только один электрон, который может принимать участие в проводимости, то полное число состояний для донорной примеси должно быть равно количеству атомов введенной примеси на единицу объема кристалла, т. е. равно Nd.
|
 Рис. 2.5. Электронный (а) и акцепторный (б) полупроводники. Рис. 2.5. Электронный (а) и акцепторный (б) полупроводники.
|
Предположим, что концентрация электронов, находящихся на уровне донорной примеси, равна пd. В этом случае концентрация ионизованных донорных атомов рd, образовавшихся в результате тепловых переходов электронов с донорных уровней в зону проводимости и имеющих положительный заряд, составит
рd = Nd - пd (2.39)
Если бы на примесном донорном уровне согласно принципу Паули могли расположиться два электрона с антипараллельными спинами, то вероятность его заполнения определялась бы функцией Ферми—Дирака (2.34), в которой вместо Е следовало поставить Еd - энергию электрона на уровне примеси. Но на уровне Еd может быть только один электрон, который может быть захвачен в зону проводимости двояким образом в зависимости от направления спина. Следовательно, нейтральное состояние донорной примеси имеет вдвое больший статистический вес по сравнению с ионизованным состоянием. Так как при отсутствии электрона на уровне донорной примеси вероятность такого состояния равна 1, то, исходя из принципа Больцмана, можно написать:
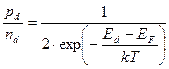 (2.40)
(2.40)
Используя (2.39), это равенство можно записать в виде
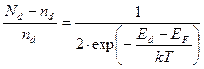 (2.41)
(2.41)
откуда следует,что концентрация электронов, находящихсянауровнях донорной примеси, равна:
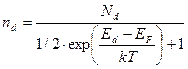
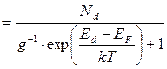 , (2.42)
, (2.42)
Где g – фактор спинового вырождения (физический смысл – число квантовых состояний с одной и той же энергией).
а концентрация положительных ионов донорной примеси на основании равенств (2.40) и (2.42) будет выражаться соотношением вида:
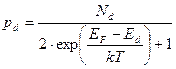
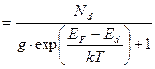 (2.43)
(2.43)
Тогда вероятность нахождения электрона на донорном уровне с энергией Еd будет определяться выражением:
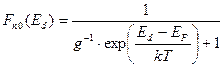 , (2.44)
, (2.44)
а функция распределения для положительных ионов донорной примеси на основании и (2.43) будет:
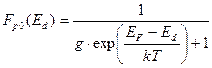 (2.45)
(2.45)
Таким образом, для одновалентной донорной примеси, для которой примесный уровень двукратно вырожден, фактор (степень) спинового вырождения g = 2.
Рассмотрим теперь акцепторный полупроводник, например кремний, легированный бором. Допустим, что концентрация введенной примеси равна Na. Энергетическая схема такого полупроводника Представлена на рис. 2.5 б.
Нейтральный атом бора с соседними атомами кремния образует три ковалентные связи, четвертая связь одного из четырех соседних атомов кремния остается незавершенной, и она, располагаясь около атома бора, ведет себя как положительная дырка. В эту незавершенную связь может перейти электрон от соседнего атома кремния, и для этого потребуется энергия, равная Еа. В результате образуется свободная дырка, а атом бора превращается в отрицательно заряженный ион бора. Таким образом, на энергетическом уровне акцепторной примеси находится один электрон с произвольным направлением спина (нейтральное состояние акцепторной примеси) либо имеется два электрона с антипараллельными спинами в случае, когда атом акцепторной примеси для укомплектования парной связи захватывает электрон из валентной зоны (ионизованное состояние акцепторной примеси). Следовательно, степень вырождения акцепторного уровня g = 2. Поэтому концентрация электронов na на уровнях акцепторной примеси (или концентрация отрицательных ионов) при данной температуре будет определяться соотношением вида
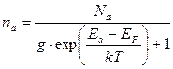 (2.46)
(2.46)
а концентрация дырок на акцепторной примеси ра соответственно будет равна:
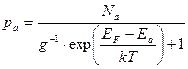 (2.46а)
(2.46а)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 5670; Нарушение авторских прав?; Мы поможем в написании вашей работы!