Изопроцессы

Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние, например (P, V, T, и m). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. Квазистатические процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (график процесса, например, в координатах p, V), каждая точка которой представляет равновесное состояние.

Переход системы из одного равновесного состояния в другое равновесное состояние называется термодинамическим процессом.

Особый интерес представляют изопроцессы. Изопроцессами называются квазистатические процессы, происходящие с идеальным газом постоянной массы, в котором еще один из трех параметров состояния (p, V или T) также не изменяется.

Из данного определения следует, что таких процессов три. Для их более подробного изучения запишем уравнение состояния (1.6.3) в виде:

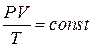, (1.7.1)

которое справедливо при m = const и называется уравнением Клапейрона.

1. Изотермический процесс (T = const).

Изотермическим процессом называется квазистатический процесс, протекающий при постоянной температуре T.

Из уравнения Клапейрона (1.7.1) следует, что для изотермического процесса произведение давления газа на его объем не изменяется (закон Бойля-Мариотта).

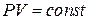. (1.7.2)

Закон Бойля-Мариотта – один из первых законов в истории науки, был открыт англичанином Р. Бойлем (1662 г.) и французом Э. Мариоттом (1676 г.).

Изотермический процесс на графике в координатах PV изображается семейством гипербол (см. рис. 1.7.1). Эти линии называются изотермами. Графики изотерм в других координатах также приведены на рис. 1.7.1.

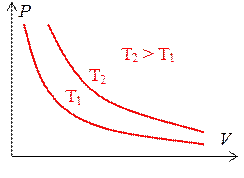
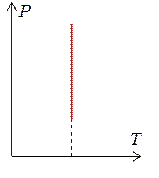
Рис. 1.7.1.

2. Изобарный процесс (P = const).

Изобарным процессом называется квазистатический процесс, протекающий при постоянном давлении P.

Из уравнения Клапейрона (1.7.1) следует, что для изобарного процесса отношение объема газа к его абсолютной температуре не изменяется (закон Гей-Люссака). Этот закон был открыт в 1802 году.

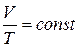. (1.7.3)

Линии, описывающие изобарный процесс называются изобарами. Графики изобар приведены на рис. 1.7.2.

Тангенс угла наклона изобары на графике в координатах VT равен . Поэтому, если угол наклона прямой a₁ > a₂, то P ₁ < P ₂.

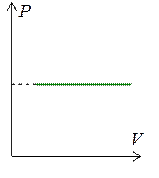
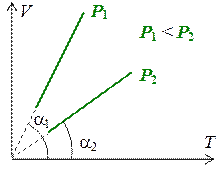
Рис. 1.7.2.

3. Изохорный процесс (V = const).

Изохорным процессом называется квазистатический процесс, протекающий при постоянном объёме V.

Из уравнения Клапейрона (1.7.1) следует, что для изохорного процесса отношение давления газа к его абсолютной температуре не изменяется (закон Шарля). Этот закон был открыт в 1787 году.

. (1.7.3)

Линии, описывающие изохорный процесс называются изохорами. Графики изохор приведены на рис. 1.7.3.

Тангенс угла наклона изохоры на графике в координатах PT равен . Поэтому, если угол наклона прямой a₁ > a₂, то V ₁ < V ₂.

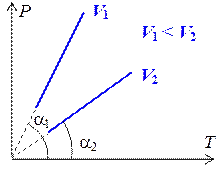
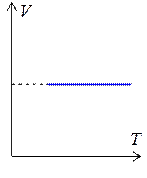
Рис. 1.7.3.

Дата добавления: 2014-01-07