Пример 2. Найти решение задачи Коши

Решение

Пример 1

Найти решение задачи Коши .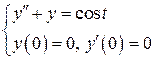

, .

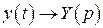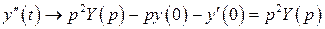Перейдем от ДУ (в оригиналах) к алгебраическому уравнению (в изображениях):

, ,

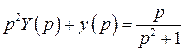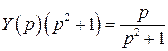– изображение искомого решения.

Найдем оригинал для :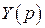

,

, ,

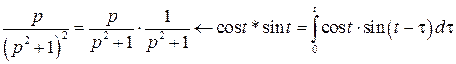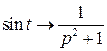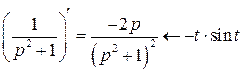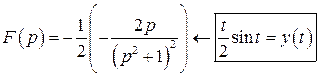
Решить операторным методом ДУ: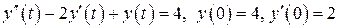

Решение.

Запишем изображающее уравнение

,

,

,

,

,

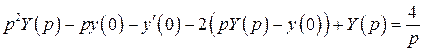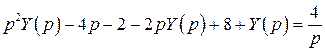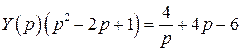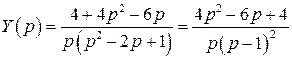Разложим полученную дробь на простейшие:

,

.

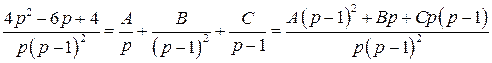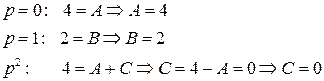
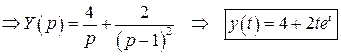Решим это же уравнение обычным методом:

,

,

, ,

.

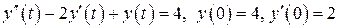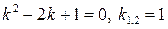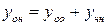
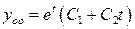
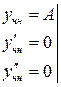
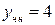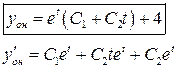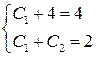
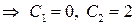
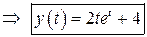Вопрос 2. Решение задачи Коши для системы линейных дифференциальных уравнений с постоянными коэффициентами операторным методом.

Описание целого ряда процессов и явлений требует одновременного рассмотрения нескольких взаимосвязанных неизвестных функций. Если эти функции зависят от одной переменной и должны удовлетворять некоторому набору дифференциальных уравнений, то задача сводится к решению систем обыкновенных дифференциальных уравнений.

Определение. Нормальной системой n дифференциальных уравнений называется система, приведенная к виду

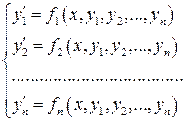, (1)

где 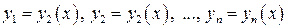– неизвестные функции, зависящие от х, т.е. система уравнений, разрешенных относительно производных от искомых функций.

Определение. Решением нормальной системы (1) на интервале 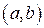изменения аргумента называется всякая система n функций

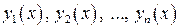
дифференцируемых на интервале 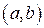, обращая уравнения системы (1) в тождество по х на этом интервале.

Рассмотрим, для наглядности, нормальную систему двух уравнений

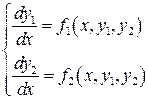. (2)

Система дифференциальных уравнений, как правило, имеет бесконечное множество решений. Для того, чтобы выделить из этого множества какое-то частное решение нужно задать начальные условия, что приводит к задаче Коши.

Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид:

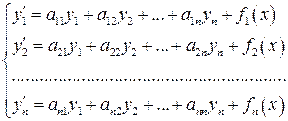, (3)

где коэффициенты 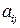– постоянные, х – аргумент, 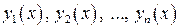– искомые функции, 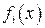– известные функции.

В случае, когда все 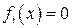, мы получим систему однородных линейных уравнений.

Задача Коши для системы ЛДУ с постоянными коэффициентами: найти решение системы уравнений (3), удовлетворяющее начальным условиям:

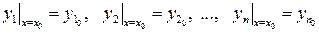. (4)

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения – путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю систему как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для него будет решением исходной системы ДУ.

Рассмотрим операторный метод на примере решения системы двух уравнений с двумя неизвестными.

Пусть дана система

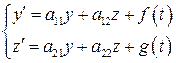. (5)

Требуется найти решение этой системы, удовлетворяющее начальным условиям

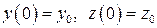. (6)

Введем обозначения:

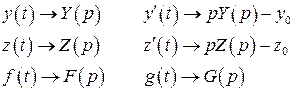
Перейдем от системы дифференциальных уравнений (в оригиналах) к системе алгебраических уравнений (7) (в изображениях)

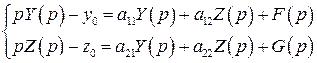. (7)

Перепишем систему в стандартном виде

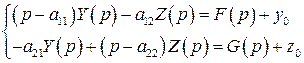. (8)

Неизвестными в системе (8) являются функци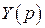и и 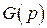. Система (8) – система линейных уравнений, ее можно решить по формулам Крамера:

,

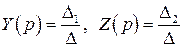где

,

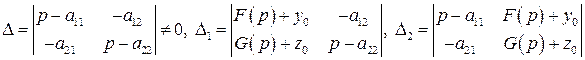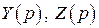– изображения функци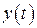й и 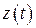, которые образуют решение системы дифференциальных уравнения.

Дата добавления: 2014-01-07