Критерий абсолютной устойчивости В.М.Попова

Абсолютная устойчивость- это устойчивость в целом нелинейной системы при задании ее нелинейностей принадлежностью к определенному классу. При этом понимается задание нелинейности не конкретной характеристикой, а в более общем виде- с точностью только до определения ее класса. Типичным случаем такого задания является задание статической нелинейной характеристики тем, что она должна находиться в пределах определеннго угла между осью абсцисс и некоторой прямой, как показано на рис.7.11. При этом конкретная форма нелинейной характеристики может быть любой, в том числе и непостоянной. При таком определении характеристики говорят, что она задана в угле (0,k). Здесь 0 и k- тангенсы углов наклона линий, ограничивающих этот угол.

Y arctgk

x

y=f(x)

Рис.7.11. Нелинейная характеристика, заданная в угле (0,k)

Исследование систем при таком неконкретном задании нелинейностей вызвано не только чисто математическими соображениями в смысле упрощения задачи, но имеет и практический смысл в тех случаях, когда нелинейности известны неточно или могут изменяться.

Критерий абсолютной устойчивости В.М.Попова, предложенный в 1959г., относится к системам, которые можно представить в виде соединения линейной части с передаточной функцией W_л(s) и безынерционного нелинейного звена f(x) (рис.7.12а). W_л^*(s) j

W_л(s)

- W_л(s)

Y X w=0

f(x)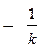

a)

b)

Рис.7.12.Структурная схема системы и преобразованная АФЧХ

Характеристика нелинейного звена является однозначной и лежит в угле (0,k). Минус на входе W_л(s) показывает, что обратная связь в системе отрицательна. Для суждения об устойчивости по этому критерию используется преобразованная амплитудно-фазовая частотная характеристика

W ^*_л(jw)=ReW_л(jw)+ jwIm W_л(jw) (7.38)
Эта характеристика получается из АФЧХ W_л(jw) линейной части системы путем умножения ординат последней на текущее значение частоты w (рис.7.12b).

Рассмотрим вначале критерий В.М.Попова, когда линейная часть системы устойчива.

Нелинейная система абсолютно устойчива, если при устойчивой линейной части системы через точку (-1/k, j0) можно провести хотя бы одну прямую линию так, чтобы вся характеристика W_л^*(jw) находилась от нее справа. Такая линия называется линией Попова. j

критерий абсолютной устойчивости не выполняется. если характеристика W_л^*(jw) охватывает точку (-1/k, j0) Критерий В.М.Попова является достаточным, т.е. он дает часть области абсолютной устойчивости и его невыполнение может не означать отсутствия абсолютной устойчивости в какой – либо другой области.

Представляет интерес сравнить условия абсолютной устойчивости В.М.Попова с условиями устойчивости линейной системы, получаемой при предположении, что характеристика f(x) в угле (0,k) является линейной. Это значит, что нелинейное звено f(x) заменяется идеальным линейным звеном с коэффициентом передачи k₀, лежащим в пределах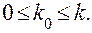

Передаточная функция для такой разомкнутой системы равна k₀W_л(s). Согласно критерию Найквиста, условие устойчивости рассматриваемой линейной системы заключается в том, что АФЧХ k₀W_л(jw) не должна охватывать точку
(-1,j0). Это эквивалентно условию, что АФЧХ W_л(jw) линейной части системы не охватывает точку (-1/k, j0). Действительно, граница устойчивости по Найквисту соответствует равенству k₀W_л(jw)=-1, т.е. W_л(jw)=-1/k₀. При изменении величины k₀ в диапазоне от 0 до k точка (-1/k₀,j0) перемещается по действительной оси -¥ до -1/k₀. Поэтому условием устойчивости линейной системы при k₀=0¸k является прохождение характеристики W_л(jw) через действительную ось правее точки (1/k,jo), т.е. непересечение ею действительной оси левее этой точки.
Характеристики W_л(jw) и W_л^*(jw) имеют одинаковые действительные части и, следовательно, пересекают действительную ось в одних и тех же точках. Поэтому сформулированное условие устойчивости линейной системы полностью относится и к характеристике W_л^*(jw).

Таким образом, достаточное условие устойчивости при произвольной форме однозначной нелинейной характеристики f(x) в угле (0,k) оказывается строже необходимого и достаточного условия в случае линейной характеристики f(x) в этом угле тем, что помимо необходимости нахождения характеристики W_л^*(jw) правее точки (-1/k,j0) требует еще возможности проведения через эту точку линии Попова.

Для того, чтобы распространить рассмотренный критерий на системы с неустойчивой линейной частью, преобразуем предварительную схему системы, как это показано на рис.7.14а. Здесь в схему введены два фиктивных звена с коэффициентом передачи k_ф. Они ничего не изменяют в системе, так как их выходные сигналы взаимно компенсируют друг друга на входе линейной части системы.

W_лф(s)

K_ф k k-k_ф

-

Ä W_л(s) k_ф

- x

y

Ä f(x)

-

k_ф

f_ф(x)

а) б)

Рис.7.14. Система с неустойчивой линейной частью

В результате получаем систему, состоящую из линейной части с передаточной функцией

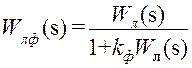(7.39)
и нелинейной части с характеристикой

f_ф(x)=f(x)-k_фx (7.40)

Выберем величину коэффициента передачи k_ф такой, чтобы за счет введенной отрицательной обратной связи вокруг W_л(s) новая линейная часть оказалась устойчивой, т.е. все полюсы передаточной функции W_лф(s) были левыми.

Отметим сразу, что если последнее не может быть осуществлено, то это уже означает отрицательный ответ на вопрос об абсолютной устойчивости исходной системы, так как при этом она оказывается неустойчивой даже при линейной характеристике f(x) любого наклона.

Применим к преобразованной системе с устойчивой линейной частью критерий абсолютной устойчивости В.М.Попова и получим следующее условие абсолютной устойчивости исходной системы с неустойчивой линейной частью:
система абсолютно устойчива, если через точку (-1/(k-k_ф),j0) можно провести прямую линию, проходящую слева от характеристики W_лф^*(jw). Абсцисса указанной точки определена в соответствии с соотношением (7.40). При этом k определяется углом, в котором задана характеристика f(x).

В соответствии с критерием В.М.Попова характеристика f_ф(x) должна лежать в угле, ограниченном с одной стороны осью абсцисс. С учетом (7.40) это означает, что характеристика f(x) должна лежать вне угла (0,k_ф). Таким образом, сформулированный критерий должен быть дополнен требованием, чтобы характеристика f(x) лежала в угле (k_ф,k), как показано на рис.7.14б. Характеристика f_ф(x) при этом будет лежать в угле (0,(k-k_ф)).

В частном случае, когда передаточная функция W_л(s) линейной части имеет мнимые или нулевые полюсы при остальных левых полюсах, изложенный критерий абсолютной устойчивости совпадает с ранее сформулированным для случая устойчивой линейной части, но должен быть дополнен двумя следующими условиями.

Во-первых, должна обеспечиваться так называемая предельная устойчивость, под которой понимается устойчивость линейной системы с передаточной функцией kW_л(s) при .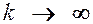

Во-вторых, исключается касание характеристикой нелинейного звена оси абсцисс, т.е. абсолютная устойчивость рассматривается в угле (e,k), где e-бесконечно малая величина.

Критерий В.М.Попова можно распространить на более общий случай нелинейности, когда характеристика f(x) лежит в угле (k₁,k₂), где k₁ может быть как положительным, так и отрицательным (рис.7.15а). Этот случай сводится к основному случаю с характеристикой f(x) в угле (0, k), если представить нелинейность в следующем виде:

f(x)=f_ф(x)+k₁x (7.41)
Очевидно, что новая нелинейность f_ф(x) лежит в угле (0, k), где k=k₂-k₁.

В результате получим схему, приведенную на рис.7.15б, где нелинейность f_ф(x) лежит в угле (0,k), а линейная часть имеет передаточную функцию

Y - Ä - W_л(s)

k₂

k₁>0 k₁

W_лф(s)

X

f_ф(x)

k₁<0

a) б)

Рис.7.15. Оценка абсолютной устойчивости при произвольном угле (k₁,k₂)

(7.42)

Дата добавления: 2014-01-07