Статистические характеристики случайных погрешностей

1. Диапазон рассеивания размеров

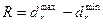
1. Эмпирическое среднее квадратическое отклонение

,

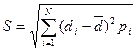N – всего деталей;

n_i – деталей с размером d_i;

– частость (вероятность) появления d_i размера;

–остаточная погрешность.

При n≥25 S≈σ

σ – среднее квадратическое отклонение генеральной совокупности. Является количественной характеристикой рассеивания размеров при обработке.

S – эмпирическая оценка σ по ограниченной выборке.

1. Законы распределения (рассеивания) действительных размеров деталей.

– Нормальный (закон Гаусса).

Так распределены случайные величины при большом числе равновероятно влияющих факторов.

Наиболее широко распространено в машиностроении: случайные погрешности измерения, линейные размеры и т.д.

Кривая Гаусса.

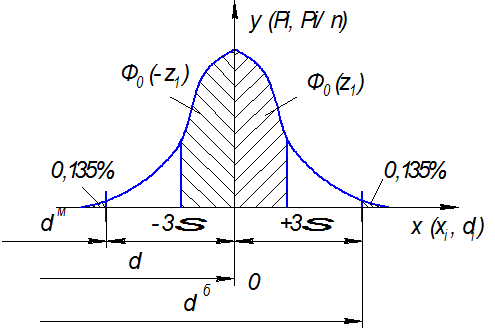
Функция плотности распределения

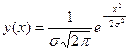
где е – основание натурального логарифма.

Нормальное распределение наиболее часто встречается при технических измерениях.

Свойство нормально распределенных случайных величин:

– отклонение от 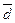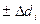встречаются одинаково часто (кривая симметрична относительно );

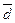– малые по величине погрешности встречаются чаще, чем больше;

– алгебраическая сумма отклонений от среднего значения равна нулю. Кривая симметрична относительно максимальной ординаты.

Математическое ожидание (центр распределения, группирования)

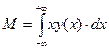
Ветви кривой уходят в , асимптотически приближаясь к оси абсцисс.

Зная функцию плотности вероятности можно определить вероятное число деталей в заданном интервале размеров.

Площадь ограничиваемая кривой и осью абсцисс = вероятности нахождения погрешности х от –∞ до +∞ =1 (100%)

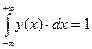
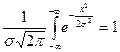
Подынтегральная функция четная, кривая симметрична относительно центра группирования.

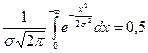
Оказывается удобно выразить случайную величину х в долях ее σ:

обозначим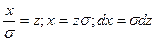

Заменив переменную и взяв предел интегрирования z, получим

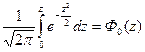
Функция Лапласа, табулирована во всех справочниках.

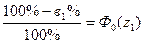
в₁% – число деталей в интервале 0–Z₁. Можно задаться и числом деталей в₁%, рассчитать Ф₀(Z₁), и по таблице определить интервал 0–Z₁.

Свойство Ф₀(Z)

Ф₀(0) = 0; Ф₀(-Z) = – Ф₀(Z)

Ф₀(-∞) = –0,5; Ф₀(∞) = +0,5.

Ф₀(3) = 0,49865

Ф₀(3)– Ф₀(-3) = 2Ф₀(3) = 0,9973

Вероятность попадания размера детали в интервал 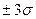равна 0,9973.

– закон равной вероятности.

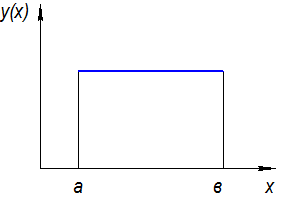
Имеется резко доминирующий фактор, равномерно изменяются: например размеры деталей при равномерном износе резца.

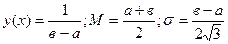
– закон треугольника (Симпсона)

2 резко доминирующих фактора.

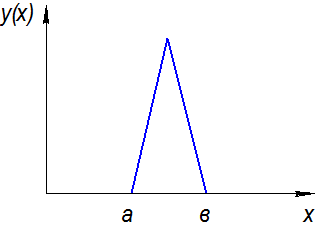
Законы могут комбинироваться:

∩+∏ =

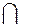
Дата добавления: 2014-01-07