I.1. Системы обыкновенных дифференциальных уравнений. Основные понятия и определения

СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

ЛЕКЦИЯ 4-5.

В общем виде система обыкновенных дифференциальных уравнений может быть записана следующим образом

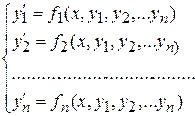(1)

где функции 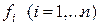определены в некоторой 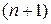мерной области D переменных 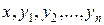. Такие системы называются нормальными системами п дифференциальных уравнений первого порядка с неизвестными функциями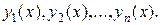

Число уравнений, входящих в систему (1), определяет ее порядок.

Решением системы (1) в интервале (а, b) называется совокупность функций 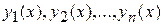, непрерывно дифференцируемых в (а, b) вместе со своими производными и обращающих каждое уравнение системы (1) в тождество.

Задача Коши для систем дифференциальных уравнений первого порядка имеет следующую формулировку. Найти решение 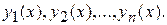системы, удовлетворяющее начальным условиям:

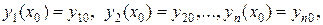(2)

где 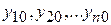– заданные числа;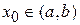

Теорема (о существовании и единственности решения задачи Коши). Если функции 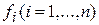непрерывны в окрестности точки 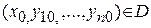и имеют непрерывные частные производные 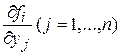, то всегда найдется некоторый интервал с центром 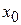, в котором существует единственное решение системы (1), удовлетворяющее начальным условиям.

Общим решением системы (1) называется совокупность 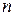функций 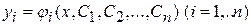, зависящих от n произвольных постоянных 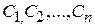и удовлетворяющих следующим условиям:

1) функции 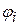определены в некоторой области изменения переменных 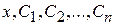и имеют непрерывные частные производные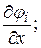

2) совокупность 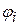является решением системы (1) при любых значениях .

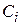3) для любых начальных условий (2) из области 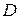, где выполняются условия теоремы Коши, всегда найдутся такие значения произвольных постоянных 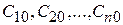, что будут справедливы равенства

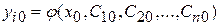
Геометрически общее решение системы представляет собой 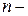параметрическое семейство плоских кривых.

Частным решением системы (1) называется решение, полученное из общего при некоторых частных значениях произвольных постоянных.

Одним из методов решения системы (1) является сведение ее к одному или нескольким дифференциальным уравнениям высших порядков (метод исключения).

Все сказанное распространяется и для систем линейных дифференциальных уравнений, которые имеют вид

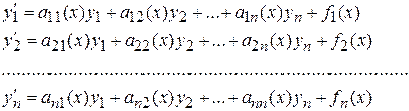(3)

где функции 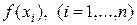обычно предполагаются непрерывными в некотором интервале 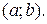Если все 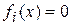, то система называется однородной, в противном случае – неоднородной. Если 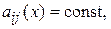то система называется линейной с постоянными коэффициентами.

Процесс нахождения общего решения системы называется ее интегрированием. Для этого, составляют характеристическое уравнение

,

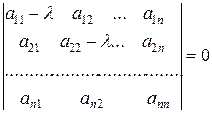где 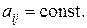Раскрывая определитель, приходим к алгебраическому уравнению степени 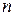относительно 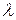с вещественными коэффициентами, которое, согласно утверждению основной теоремы алгебры, имеет ровно 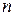корней вещественных и комплексных с учетом их кратности.

При этом возможны следующие случаи.

1. Корни характеристического уравнения – вещественные и различные. Обозначим их через 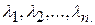Известно, что каждому корню 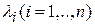соответствует частное решение вида

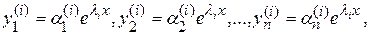(4)

где коэффициенты 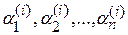определяются из систем линейных алгебраических уравнений

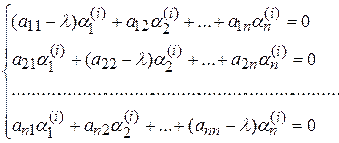. (5)

Все частные решения вида (4) образуют фундаментальную систему решений. Общее решение однородной системы с постоянными коэффициентами, получаемой из системы (3) при 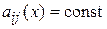, , 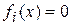представляет собой следующую совокупность функций, являющихся линейной комбинацией решений (4):

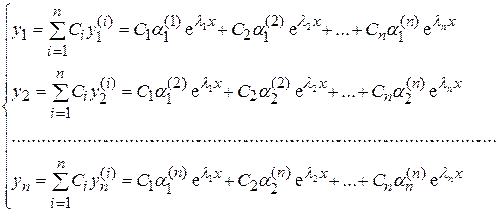
где 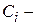произвольные постоянные.

2. Корни 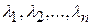характеристического уравнения – различные, но среди них имеются комплексные. Известно, что в этом случае каждой паре комплексно-сопряженных корней 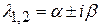характеристического уравнения соответствует пара частных решений:

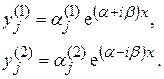(6)

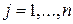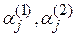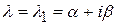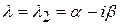где ; коэффициенты определяются из системы (5) соответственно для и . Коэффициенты 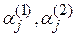оказываются, как правило, комплексными числами, а соответствующие им функции 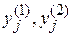– комплексными функциями. Выделяя мнимую и вещественную части функци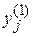й и 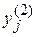, и пользуясь тем, что для линейных уравнений с вещественными коэффициентами и мнимая, и вещественная части решения также являются решениями, можно получить пару частных вещественных решений однородной системы.

3. Среди корней 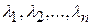характеристического уравнения имеются кратные. Пусть 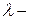корень кратности 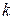характеристического уравнения. Тогда решение системы (2) (для которой 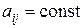, 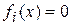(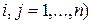), соответствующее этому 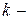кратному корню, ищем в виде:

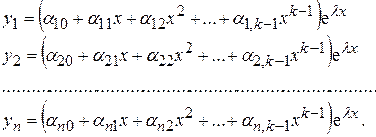(7)

Числа 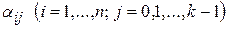находим следующим образом: подставляем функции 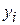из (7) и их производные в исходную систему (3) при указанных ограничениях на 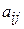и 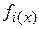, а затем, после сокращения на 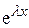, приравняем коэффициенты при одинаковых степенях 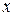в левых и правых частях полученных равенств. В результате проведенной процедуры из всех чисел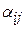 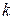всегда остаются в качестве свободных параметров, которые принимаются как произвольные постоянные.

Решения из фундаментальной системы, соответствующие простым (некратным) корням характеристического уравнения, определяются так, как это было показано в п.п. 1 и 2.

Дата добавления: 2014-01-07