I.3. Метод исключения

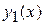При выполнении некоторых условий всегда можно исключить все неизвестные функции, кроме одной, например , и получить для одно линейное неоднородное дифференциальное уравнение с постоянными коэффициентами (если в системе (3) ) порядка 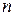. Решив его, найдем все остальные неизвестные функции 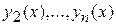с помощью операции дифференцирования. Для этого, дифференцируем по 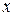обе части первого уравнения системы (3) (считая ), затем вместо 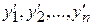подставляем их значения из системы (3). Получаем:

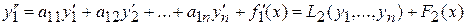, (8)

где 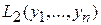обозначает известную линейную комбинацию с постоянными коэффициентами функций 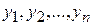, а линейную комбинацию функций и . Дифференцируя обе части уравнения (8) по 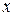, опять получаем линейное неоднородное уравнение

.

Продолжая процесс, находим

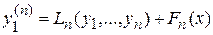
В результате получаем систему 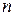уравнений:

(9)

Первые 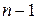уравнений системы (9) разрешаем относительно функций 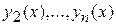(это, как правило, возможно). Очевидно, что эти функции выражаются через :

(10)

Подставляя выражения для 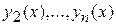из системы (10) в последнее уравнение системы (9), приходим к линейному неоднородному дифференциальному уравнению 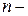го порядка с постоянными коэффициентами

,

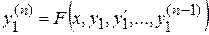общее решение, которого определяется с помощью известных методов:

. (11)

Дифференцируя последнее соотношение, 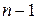раз по 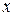, находим производные , подставляем их в систему (10) и получаем вместе с функцией (11) общее решение исходной системы:

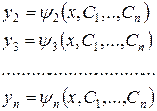(12)

Для решения задачи Коши с учетом системы (11) – (12) и заданных начальных условий находим значения произвольных постоянных и подставляем их в систему (11) – (12).

Дата добавления: 2014-01-07