Формула полной вероятности. Формула Байеса

Рассмотрим вероятность события А, которое может наступить при условии появления одного из попарно независимых событий 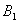, , 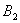…, , 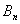образующих полную группу. События 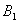, , 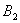…, 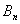в этом случае называются гипотезами. Вероятности появления гипотез P ( 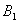), P ( 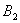), …, P ( 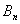), а также условные вероятности появления события А при наступлении каждой гипотезы 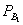(А), 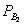(А), …, 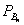(А) будем считать известными.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из попарно независимых событий 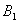, , 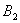…, , 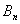образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

P(А)= P (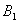)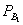 (А)+P (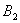)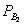 (А) +… P (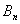)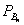 (А)= .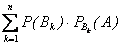

Эту формулу называют формулой полной вероятности.

Пусть известно, что в результате реализации испытания событие А наступило. Однако какая именно гипотеза 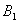, , 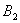…, 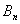привела к появлению события А, неизвестно. Необходимо найти условные вероятности (), (), …, ().

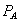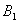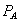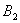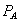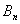По теореме умножения вероятностей

P(А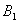 ) = P(А)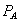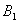 ( ) = P ( 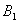)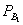 (А).

Отсюда,

( )= .

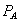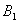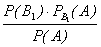Подставив P(А) по формуле полной вероятности, получим

( )= ,

( )=

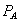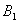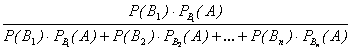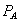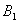Аналогично находятся условные вероятности гипотез , …, .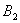

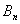Итак,

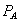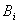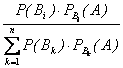( )= (i =1, 2, …, n).

Полученные формулы называются формулами Байеса.

Формулы Байеса оценивают вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. В отличие от «доопытных» вероятностей P ( 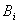), 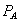( 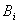) (i =1, 2, …, n) называют «послеопытными» вероятностями гипотез. В общем случае P ( ) ( ).

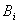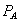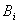Пример 5.26. В первой коробке находятся 10 патронов, 4 из которых являются холостыми, во второй коробке – 15 патронов, из которых 3 холостых. Найти вероятность того, что взятый наудачу патрон будет холостым. Найти вероятность того, что патрон был взят из первой коробки, если он оказался холостым.

Решение. Событие А – то, что взятый наудачу патрон будет холостым – может наступить при условии появления двух гипотез: патрон берется из первой коробки (обозначим эту гипотезу через 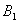), патрон берется из второй коробки (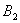). Вероятность этих гипотез одинакова P (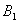) =P (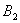)= 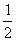. Условная вероятность того, что из первой коробки будет извлечен холостой патрон 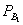(А)= 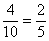. Условная вероятность того, что холостой патрон будет извлечен из второй коробки 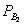(А)= .

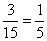Вероятность события А рассчитывается по формуле полной вероятности:

P(А)= P ( 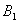)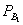 (А)+P ( 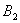)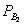 (А)=  +  = .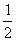

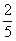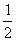
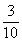Если вытащенный патрон оказался холостым, то вероятность того, что он был взят из первой коробки 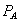(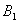) определяется по формуле Байеса:

( )= = .

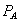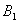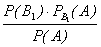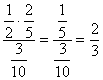Дата добавления: 2014-01-07