
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Бернулли. Пусть производится n независимых друг от друга испытаний, в каждом из которых случайное событие А может либо произойти
|
|
|
|
Пусть производится n независимых друг от друга испытаний, в каждом из которых случайное событие А может либо произойти, либо не произойти. Результат каждого испытания — случайное событие, вероятность которого естественно считать независящей от результатов других бросаний. Вероятность того, что событие А состоится в каждом испытании одна и та же и равна p. Следовательно, вероятность того, что событие А не произойдет, равна 1– р. Обозначим эту величину через q =1– р. Зададимся вопросом, какова будет вероятность того, что при n испытаниях событие А наступит в k из них и, соответственно, в n-k испытаниях не наступит?
Для подсчета вероятности  пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n-k испытаниях. Так как испытания независимы, то по теореме умножения вероятностей получим вероятность такого сложного события равной
пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n-k испытаниях. Так как испытания независимы, то по теореме умножения вероятностей получим вероятность такого сложного события равной 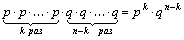 . Наше искомое событие, состоящее в наступлении А в любых k испытаниях из общего числа n испытаний, разбивается на вышеупомянутые сложные несовместные события, количество которых
. Наше искомое событие, состоящее в наступлении А в любых k испытаниях из общего числа n испытаний, разбивается на вышеупомянутые сложные несовместные события, количество которых 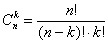 . Например, если n =4, а k =2, то такие события: AA
. Например, если n =4, а k =2, то такие события: AA 
 , А
, А 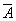 А
А 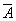 , А
, А 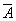
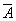 А,
А, 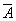 A
A 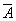 А,
А, 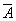
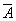 АА,
АА, 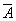 АА
АА 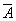 . В этих записях А обозначает наступление события, а
. В этих записях А обозначает наступление события, а 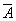 - ненаступление. Так AA
- ненаступление. Так AA 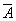
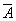 означает, что интересующее нас событие наступило в 1 и 2 испытании, а в 3 и 4 – не наступило.
означает, что интересующее нас событие наступило в 1 и 2 испытании, а в 3 и 4 – не наступило.
По теореме сложения вероятностей для несовместных событий вероятность наступления события А в k из n испытаниях 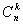
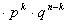 (сумма
(сумма 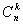 одинаковых слагаемых, каждое из которых равно
одинаковых слагаемых, каждое из которых равно 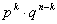 ).
).
Таким образом,

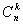
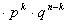 (0 k n). (5.7)
(0 k n). (5.7)
Полученная формула носит название формулы Бернулли.
Ясно, что несовместные сложные события, состоящие в появлении события А 0 раз, 1 раз, 2 раза, …, n раз в n испытаниях образуют полную группу событий. Поэтому сумма вероятностей этих событий 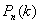 для 0 k n равна единице:
для 0 k n равна единице:
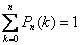 .
.
Это соотношение можно получить, непосредственно вычислив сумму 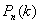 , применив формулу бинома Ньютона (
, применив формулу бинома Ньютона ( ):
):
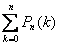 =
= 
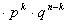 =
= 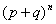 =
= 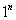 =1.
=1.
Пример 5.27. Производится 6 выстрелов по мишени. Вероятность попадания в мишень при каждом выстреле 0,7. Какова вероятность, что после этого в мишени окажется 4 пробоины? Какова вероятность поражения мишени хотя бы одним выстрелом?
Решение. Для расчета вероятности 4 попаданий из 6 выстрелов воспользуемся формулой Бернулли. Вероятность попадания при одном выстреле p =0,7. q = 1– р= 0,3.

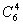
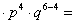

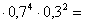
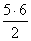
 0,32.
0,32.
Вероятность попадания в мишень хотя бы один раз по теореме сложения равна сумме вероятностей попадания в мишень одни раз, два раза, три раза, четыре раза, пять раз и шесть раз, т.к. эти события несовместны. Каждую из этих вероятностей можно вычислить по формуле Бернулли. Но значительно проще найти искомую вероятность через вероятность противоположного события – непопадания в мишень ни разу.


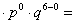


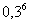
 0,0007.
0,0007.
Таким образом, вероятность поражения мишени хотя бы одним выстрелом 1–0,0007 = 0,9993.
В заключение этой главы проведем аналогии между основными понятиями и операциями теории множеств, математической логики и теории вероятностей.
| Теория множеств Основной объект – множество | Математическая логика Основной объект – высказывание | Теория вероятностей Основной объект – событие |
| Объединение множеств | Дизъюнкция высказываний | Сумма событий |
| Пересечение множеств | Конъюнкция высказываний | Произведение событий |
| Дополнение множества | Отрицание высказывания | Противоположное событие |
| Универсальное множество | Абсолютно истинное высказывание | Достоверное событие |
| Пустое множество | Абсолютно ложное высказывание | Невозможное событие |
Операции объединения и пересечения множеств, дизъюнкция и конъюнкция высказываний, сумма и произведение событий обладают коммутативным, ассоциативным, дистрибутивным свойствами. Это еще раз подчеркивает глубокую связь между отдельными разделами математики, переход этой науки на высокий уровень абстракции изучения объектов.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!