Странные хаотические аттракторы

В этом разделе будут приведены примеры, которые иллюстри­руют принципиальную возможность хаоса как стационарного ре­жима динамики диссипативных систем. (Имеется в виду стацио­нарность в статистическом смысле, когда постоянны лишь усред­ненные за достаточно большой интервал времени статистические характеристики динамики.) Это двумерные и трехмерные модель­ные отображения, в фазовом пространстве которых имеется притя­гивающее множество сложной структуры, называемое странным хаотическим аттрактором (иногда один из двух эпитетов опус­кают).

Обобщенное отображение пекаря. Вернемся к рассмотренному в предыдущем разделе отображению пекаря и предпримем неко­торую его модификацию. Пусть первоначальный разрез «куска те­ста» — единичного квадрата производится в отношении, при этом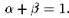, Далее оба куска растягиваются по горизонтали до

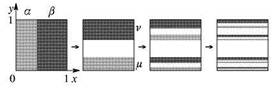
Рис. 2.9. Геометрическая иллюстрация действия обобщенного отображения пе­каря (2.21); показаны три последовательные итерации. Можно видеть, как шаг за шагом формируется кантороподобная структура аттрактора

единичной длины, сжимаются по вертикали, так что их высоты будут соответственно, и располагаются в преде-

лах единичного квадрата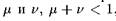у верхнего и нижнего его края (рис. 2.9). В аналитической форме предлагаемое отображение записываетсяследующим образом:

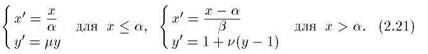
Заметим, что суммарная площадь прямоугольников, образовав­шихся после ппименения преобразования, уменьшилась на фак­тор, т. е. оно уже не относится к классу сохраня­ющих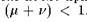площадь. Это диссипативная система с двумерным фазо­вым пространством. На рис. 2.9 показано, что происходит при нескольких последовательных итерациях обобщенного отображе­ния пекаря. Образуется характерная система горизонтальных по­лос, суммарная ширина которых убывает с ростом числа итераций как. Объект, возникающий в пределе бесконечно боль­шогочисла итераций, в сечении представляет собой так называе­мое двухмасштабное канторово множество. Процедура его постро­ения состоит в том, что берется единичный отрезок, делится в отношении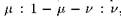, и средняя часть исключается. То же самое проделывается с двумя оставшимися отрезками, затем с каждым из отрезков, возникших на предыдущем шаге, и т. д. Заметим, что классическое множество Кантора отвечает частному случаю данного построения, а именно, выбору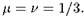

Аттрактор имеет нулевую меру, поскольку суммарная площадь полос на га-м шаге дается выражением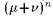и стремится к нулю

при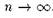, так как. Все точки исходного единичного

квадрата приближаются к аттрактору. В то же время аттрактор обладает тем свойством, что соседние по горизонтали точки удаля­ются друг от друга при последовательных итерациях, т. е. имеет место неустойчивость. Отметьте сочетание устойчивости в смы­сле наличия притяжения к аттрактору и неустойчивости в смы­сле разбегания точек на аттракторе. Поперечная структура в виде канторова или кантороподобного множества очень характерна для странных аттракторов. Обобщенное отображение пекаря является очень простым для анализа и будет использоваться в последую­щих лекциях в качестве одного из основных примеров. Некоторую неудовлетворенность, однако, может вызвать тот момент, что это отображение не является непрерывным.

Аттрактор Плыкина. Рассмотрим пример двумерного отобра­жения, обладающего свойством непрерывности и имеющего хао­тический аттрактор (Плыкин, 1980). Этот пример позволяет уяс­нить важную концепцию гиперболичности — свойства, наличие которого позволяет строго математически обосновать присутствие хаоса.

Рассмотрим область R на плоскости (ж, у), показанную на рис. 2.10а. Она состоит из квадрата и трех полудисков с полукруг­лыми вырезами. Область покрыта штриховкой, показывающейзаданное на ней поле направлений. Определим двумерное отобра­жение так, чтобы результатом его действия на точки области R была фигура, показанная на рис. 2.106". Заметьте, что поле напра­влений, возникающее после применения отображения, совпадает с исходным.

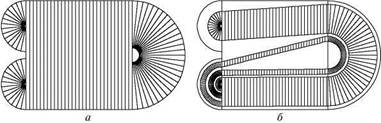
Рис. 2.10. Исходная область с определенным на ней полем направлений (а) и результат ее преобразования за один шаг отображения Плыкина (б)

На рис. 2.11 показано, что получается при многократном дей­ствии описанного отображения. Точки, заполнявшие в начальный момент область R, сконцентрирова­лись на аттракторе, который пред­ставляет собой некоторое сложно и тонко устроенное множество.

Динамика отображения Плыкина проясняется в свете следующего на­блюдения. Рассмотрим точки како­го-либо одного отрезка из числа обра­зующих штриховку на рис. 2.10а. Нетрудно видеть, что все эти точки будут демонстрировать одну и ту же динамику в том смысле, что будут одновременно посещать каждую из подобластей (квадрат и три полудиска), из которых построена область R. Если мы отождествим точки, принадлежащие каждому

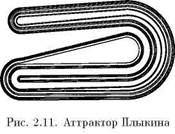
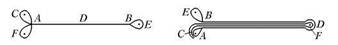
Рис. 2.12. Резиновая нить, представляющая топологию фазового пространства для одномерного аналога отображения Плыкина (слева), и ее преобразование за один шаг отображения (справа)

определенному отрезку, то вместо динамики в двумерном фазовом пространстве можем рассматривать одномерную динамику. Фазо­вым пространством для этой одномерной динамики служит «ре­зиновая нить», имеющая две петли на одном конце и одну петлю на другом (рис. 2.12). Представим себе, что эта нить натянута на три гвоздика. Один шаг итераций будет состоять в том, что мы определенным образом растягиваем нить и вновь натягиваем ее на те же гвоздики. Попробуйте изготовить модель из резино­вой нити и, используя рис. 2.12, воспроизвести один или (если удастся) больше шагов преобразования.

Аттрактор Смейла-Вильямса. Пример хаотического аттрактора, получивший наименование соленоид Смейла-Вильямса, реали­зуется в трехмерном отображении, которое строится следующим образом. Рассмотрим трехмерную область в форме тора (рис. 2.13). Представляя его для наглядности как резиновый бублик, растянем

Рис. 2.13. Первые два шага построения аттрактора Смейла-Вильямса

его в длину, сложим вдвое и вложим в исходный тор. Чтобы он там поместился, приходится предположить, что в ходе процедуры общий объем «бублика» уменьшается — площадь поперечного се­чения должна уменьшиться более чем в два раза.

На рис. 2.14 показано, как выглядит поперечное сечение ис­ходного тора после однократного и двукратного применения ото­бражения. Это похоже на процедуру построения множества Кан­тора: на каждом шаге в сечении имеется некоторое число дис­ков. Очередной шаг построения состоит в том, что внутри каждого

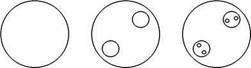
Рис. 2.14. Вид сечения аттрактора Смейла-Вильямса на первых шагах его по­строения

диска выделяются две меньшие области в форме дисков, которые оставляются для следующего шага, а все остальное множество ис­ключается. То, что останется в итоге, и есть сечение аттрактора Смейла-Вильямса. Имея в виду описанную геометрическую конструкцию, можно предложить аналитическую форму отображения. Ее удобно пред­ставить в цилиндрических координатах, которые связаны с обычными декартовыми координатами (ж, у, z) как

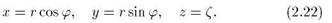
Тогда подходящей формой отображения будет

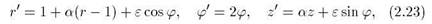
гдеПоверхность исходного тора в параметрической форме задается уравнениями

На рис. 2.15 показан портрет аттрактора, построенный пу­тем многократных итераций отображе­ния (2.23).

Приведенные примеры аттракторов Плыкина и Смейла-Вильямса сконст­руированы так, чтобы они обладали свойством, называемым гиперболич­ностью.

Когда говорят, что аттрактор какой-либо динамической системы гиперболиче­ский, то имеют в виду, что все принадлежа­щие ему траектории гиперболические (седловые), т.е. их окрестность устроена так, как показано на рис. 2.16. Возьмем лю­бую траекторию на аттракторе и рассмо­трим всевозможные близкие к ней возмущенные траектории. В линей­ном приближении среди них выделяется класс траекторий (I), которые приближаются к исходной, причем в среднем по экспоненте, и класс тра­екторий (II), приближающихся к исходной в обратном времени, тоже в среднем по экспоненте. Поскольку речь идет о рассмотрении дина­мики около исходной траектории в линейном приближении, то любой из множества инфинитезимально возмущенных траекторий сопоставляется элемент линейного векторного пространства (математики называют его касательным пространством), причем все множество исчерпывается всевозможными суперпозициями векторов, ассоциирующихся с упомя­нутыми выше возмущениями класса I и П. Подчеркнем еще раз, что так должна быть устроена окрестность у всех принадлежащих аттрактору траекторий.

Доказано, что системы, обладающие свойством гиперболично­сти, структурно устойчивы, иными словами, это свойство грубое. Если некоторая система имеет гиперболический аттрактор, то это будет справедливо и для систем, полученных произвольным до­статочно малым непрерывным возмущением исходной системы. Исходя из предположения о гиперболичности аттрактора, можно строго доказать присутствие всех других свойств, являющихся су­щественными атрибутами хаоса. Будучи принятым за аксиома-

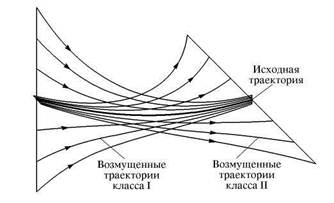
Рис. 2.16. К пояснению устройства окрестности гиперболической (седловой) тра­ектории

тически данное, свойство гиперболичности служит основой для построения теории так называемых У-систем Аносова. К сожа­лению, известные реалистичные примеры странных аттракторов (см. следующие лекции) гиперболическими в этом строгом смысле не являются.

Дата добавления: 2014-01-07