Выбор новых координат

Введем обозначения:

.

Записывая их в векторно-матричной форме, будем иметь

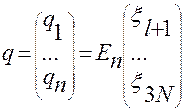. (2.4.6)

Возьмем переменные в качестве новых координат для задания положения 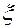механической системы.

На формулу (2.4.6) будем смотреть как на формулу связи новых координат со старыми:

.

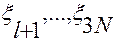Из нее легко находится зависимость координат 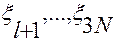от переменных .

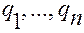Зависимости координат 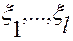от переменных 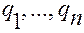получим из соотношений (2.4.5)

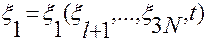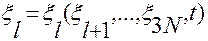,..., . (2.4.5)

Объединяя их с (2.4.6), можем записать

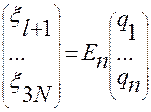, , (2.4.7)

где 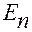— единичная матрица размерности ,

.

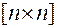Окончательно, в векторном виде система соотношений (2.4.7) запишется так:

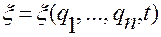. (2.4.8)

Если сопоставить систему (2.4.8) с (2.4.6)

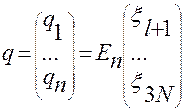, (2.4.6)

то легко заметить, что соотношения (2.4.6) образуют обратную зависимость переменных от переменных .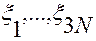

Эту зависимость будем записывать в виде

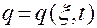. (2.4.9)

Таким образом, для описания любого положения 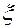механической системы вместо его координат 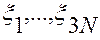ввели 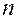новых координат вектора 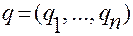, которые связаны с координатами 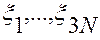вектора 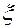следующими условиями.

1. Существует вектор-функция 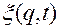, однозначно связывающая переменные 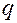и 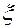(см. (2.4.8)),

.

2. Функция — однозначная, дважды непрерывно дифференцируемая по совокупности переменных и .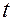

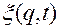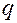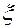3. Существует обратная по отношению функция , задающая зависимость координат вектора от и 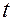(см. (2.4.9))

.

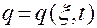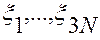4. Функция — однозначная, дважды непрерывно дифференцируемая по совокупности переменных и .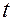

5. Матрица Якоби, вычисленная по отношению к функциям 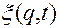по переменным 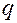, имеет ранг, равный .

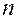6. Подстановка функций в уравнения связей (2.4.4)

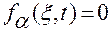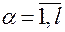, (2.4.4)

обращает эти уравнения в тождества по переменным и .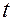

Выполнение первых четырех условий показано выше.

· Условие 5 проверяется по формуле (2.4.7):

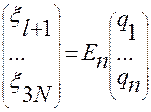, . (2.4.7)

Эта формула дает явное выражение составляющих элементов вектор-функции .

Из нее следует, что последние 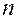строк матрицы Якоби образуют блок

,

который имеет .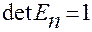

· Условие 6 вытекает из построения соотношений (2.4.5) (см. п.2.1):

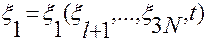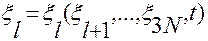,..., . (2.4.5)

Дата добавления: 2014-01-07