Малая выборка

В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые при «больших» выборках, становятся не подходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

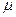МВ = 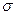/ Ön-1

Предельная ошибка малой выборки

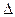МВ = t *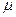МВ

В этом случае коэффициент доверия t находится по таблице распределения Стьюдента.

Пример:

Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.

Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.

1. Среднее значение признака в выборке равно

= åx / n = 8,5 + 8,0 + 7,8+9,0+7,2+6,2+8,4+6,6 / 8 = 7,71 (ч.)

2. Значение среднего квадратического отклонения составляет

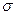МВ = Öå(x-)² /n

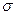МВ = Ö(8,5-7,71) ² + (8,0— 7,71) ² + (6,6 — 7,71) ² …/ 8 = 0,9102

3. Средняя ошибка выборки

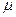МВ = 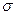/ Ön-1 = 0,9102 / Ö7 = 0,344 (ч.)

4. t = 2,365 по таблице коэффициента Стьюдента при n=8 и с вероятностью p = 0,95.

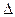МВ = t *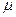МВ = 0,344 * 2,365 = 0,81 (ч.)

5. Доверительный интервал для среднего значения признака в генеральной совокупности

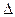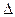- МВ + МВ

7,71 – 0,81 7,71 + 0,81

6,9 8,5

Ответ. С вероятностью 0,95 можно утверждать, что затраты времени на подготовку к контрольной работы находятся в интервале от 6,9 до 8,5 часа.

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц (таблица Ошибка! Источник ссылки не найден.):

Таблица 2.

Результаты бесповторного выборочного наблюдения на предприятии

Доход, у.е.	до 300	300-500	500-700	700-1000	более 1000
Число рабочих

С вероятностью 0,950 определить:

1) среднемесячный размер дохода работников данного предприятия;

2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;

3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;

4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.

Решение. Для расчета обобщающих характеристик выборки построим вспомогательную таблицу Ошибка! Источник ссылки не найден..

Таблица 3.

Вспомогательные расчеты для решения задачи

X	f	Х’	X ’ f	(Х ’ -)^2	(Х’ -)^2f
до 300
300 - 500
500 - 700
700 - 1000
более 1000
Итого

рассчитаем средний доход в выборке: = 57100/100 = 571 (у.е.).

Применив формулу Ошибка! Источник ссылки не найден. и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: 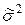= 4285900/100 = 42859.

Теперь можно определить среднюю ошибку выборки по формуле Ошибка! Источник ссылки не найден.: 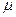= = 19,640 (у.е.).

В нашей задаче = 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле Ошибка! Источник ссылки не найден.:

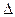= 1,96*19,64 = 38,494 (у.е.).

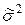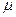Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в ГС необходимо определить их долю: w = 20/100 = 0,2 или 20%, а затем ее дисперсию по формуле = w(1-w) = 0,2*(1–0,2) = 0,16. Тогда можно рассчитать среднюю ошибку выборки по формуле Ошибка! Источник ссылки не найден.: = = 0,038 или 3,8%. А затем и предельную ошибку выборки по формуле Ошибка! Источник ссылки не найден.:

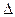= 1,96*0,038 = 0,075 или 7,5%.

Доверительный интервал среднего дохода находим по формуле Ошибка! Источник ссылки не найден.:

571-38,494571+38,494 или 532,506 у.е. 609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.

Аналогично определяем доверительный интервал для доли по формуле Ошибка! Источник ссылки не найден.:

0,2-0,075 p 0,2+0,075 или 0,125 p 0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.

В нашей задаче выборка бесповторная, значит, воспользуемся формулой Ошибка! Источник ссылки не найден., в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих (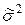= 42859) и доли рабочих с доходами более 700 у.е. (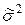= 0,16):

n_б/повт = 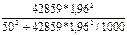= 62 (чел.), n_б/повт= 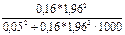= 197 (чел.).

Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.

Дата добавления: 2014-01-07