Проверка статистических гипотез

Оценивание параметров.

Основные задачи статистики

Лекция № 9

Назначение статистических методов состоит в том, чтобы по выборкам ограниченного объема делать обоснованные выводы о свойствах генеральных совокупностей, из которых эти выборки были извле

чены. При этом возникает две основные задачи:

Первая задача заключается в получении по выборочным данным оценок параметров генеральных совокупностей посредством каких-либо подходящих функций от элементов выборок. Это т.н. параметризация.

Параметрами (статистическими характеристиками) называются все подлежащие определению величины генеральной совокупности.

Примеры параметров: вероятности событий, математические ожидания, дисперсии.

Оценка – это найденное по выборочным данным значение параметра.

Статистические характеристики (параметры) вообще принято обозначать буквой 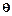, а их оценки - .

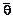Термин «оценка» используется вследствие того, что из-за случайного характера выборочных исследований в принципе невозможно гарантировать не выход ошибки параметризации из любых наперед заданных пределов. Поэтому предпочитают говорить не о приближенном значении параметра, а о получении наилучшей среди возможных оцен-

ке его величины.

На рисунке 9.1 параметром 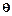является дисперсия σ²(х), а его оценкой 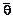- эмпирическая дисперсия s²(х).

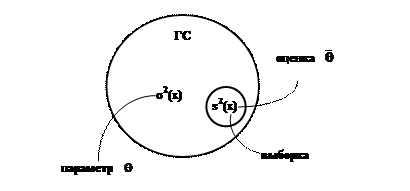
Рисунок 9.1 – Параметр и его оценка

Оценив по выборочным (эмпирическим) данным тот или иной параметр, нужно выяснить, насколько согласуется с опытными данными гипотеза о том, что параметры 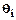действительно имеют те значения, которые получены в результате их оценивания. Это – задача проверки статистических гипотез.

Дата добавления: 2014-01-07