Михайлова

Графоаналитический критерий устойчивости

Частотные критерии устойчивости

Для получения этого критерия необходимо сформировать функцию F(jw), которая получается из характеристического уравнения системы заменой оператора P на мнимый параметр jw:

F (jw) = 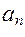(jw)ⁿ + (jw)^n-1 +... + jw +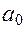. (9.10)

Выделив из выражения (9.10) вещественную и мнимую части, можно записать

F (jw) = X (w) + jY (w). (9.11)

Полученная комплексная функция может быть представлена комплексным вектором. Конец вектора при изменении w от 0 до ¥ опишет на комплексной плоскости некоторую кривую, которая называется кривой Михайлова. Очевидно, что эта кривая начинается в точке Х (0) = 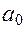, jY (0) = 0. При увеличении w от 0 до ¥ кривая, двигаясь против часовой стрелки, проходит ²n² квадрантов, уходя в ²n²-м квадранте в бесконечность (n - порядок характеристического уравнения).

Согласно критерию Михайлова, линейная система n-го порядка будет устойчива, если кривая Михайлова, начинаясь на положительной вещественной полуоси на комплексной плоскости, проходит последовательно против часовой стрелки n квадрантов, охватывая начало координат и уходя в n-м квадранте в бесконечность.

Графически кривая Михайлова строится по точкам, которые получаются аналитическим расчетом координат Х и jY при различных значениях w. В качестве примера на рис. 9.6 приведены кривые Михайлова для систем шестого порядка.

График (а) соответствует устойчивой системе, (б) - неустойчивой, (в) (сплошная линия) относится к системе, находящейся на границе устойчивости. Следует отметить, что прохождение кривой Михайлова через начало координат не всегда соответствует граничному случаю. Система тогда может быть и неустойчивой, что имеет место, если кривая Михайлова уходит в бесконечность, не достигнув шестого квадранта.

Достоинством графоаналитического критерия Михайлова является его наглядность. Он позволяет легко оценить необходимое направление изменения какого-либо параметра системы управления для обеспечения ее устойчивости (рис. 9.6, в, сплошная линия; кривые 1, 2 - влияние какого-то параметра системы).

Критерий Михайлова применим для исследования устойчивости как замкнутых, так и разомкнутых систем.

Дата добавления: 2014-01-07