Линии и поверхности уровня

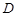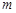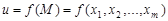Определение. Пусть на множестве точек -мерного евклидова пространства определена функция . Множество точек 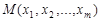удовлетворяющих уравнению

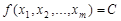, (2)

где 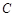— некоторая постоянная, называется множеством уровня функции , соответствующим данному значению 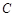. Другими словами, в любой точке множества уровня функция принимает одно и то же значение, равное .

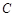В случае функции двух переменных 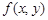уравнение (2) принимает вид

и задает некоторую линию на плоскости 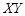, поэтому множество уровня называют линией уровня.

Экономические процессы нередко иллюстрируются графиками линий уровня функции двух переменных. Для некоторых функций линии уровня имеют свои названия. Так, например, линии уровня производственной функции называются изоквантами, а функции полезности — кривыми безразличия.

В случае трех переменных уравнение 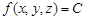— это уравнение поверхности в пространстве , и множество уровня называют поверхностью уровня.

Дата добавления: 2014-01-07