Предельное значение функций многих переменных

Пусть функция 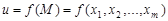определена на множестве 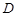точек 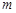-мерного евклидова пространства , а точка 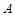является предельной точкой множества .

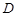Точка 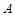, которая может и не принадлежать 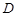, называется предельной точкой множества 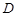, если можно выделить последовательность точек, принадлежащих 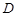, сходящуюся к .

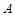Определение. Число называется предельным значением функции 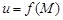в точке 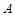(или пределом функции при 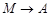), если для любой сходящейся к 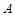последовательности 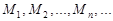точек множества 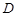, элементы которой отличны от 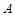, соответствующая

последовательность значений функции 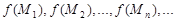сходится к .

Как и в случае функции одной переменной, можно дать другое эквивалентное определение предельного значения функции многих переменных, используя «» терминологию.

Определение. Число называется предельным значением функции 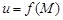в точке 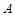, если для любого положительного числа 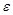можно указать такое положительное число 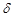что для всех точек 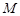из области определения функции, удовлетворяющих условию выполняется неравенство .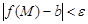

Для обозначения предельного значения функции 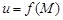в точке используется следующая символика

.

Арифметические операции над функциями многих переменных, имеющими предельное значение в точке приводят к функциям, также имеющим предельное значение в точке . Справедлива следующая теорема.

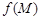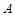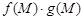Теорема. Пусть функции и имеют в точке предельные значения и . Тогда функции , и 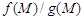имеют в точке 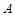предельные значения (частное при условии, что ), равные соответственно 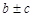, и .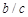

Дата добавления: 2014-01-07