Лекция № 8. 1. Определение с помощью дифрактометра интегральной отражающей способности монокристаллов и определение величины структурных множителей -

1. Определение с помощью дифрактометра интегральной отражающей способности монокристаллов и определение величины структурных множителей - .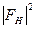

Точность установления структуры ячейки кристалла зависит от точности измерения интегральных интенсивностей. Поэтому выбор оптимальных условий сканирования объема обратного пространства вокруг узла ОР, участвующего в отражении во многом определяет точность измерения 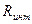и соответственно 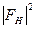. Наличие определенного спектрального интервала рабочего излучения, мозаичности изучаемого монокристалла, расходимости падающего и отраженного пучков определяет угловой интервал сканирования кристалла и счетчика и апертуру последнего. Простое увеличение этих параметров т.е. увеличение сканируемого объема обратного пространства приводит к увеличению вклада фона в измеряемую интенсивность, что приводит к уменьшению чувствительности и точности измерения .

Напомним, что при измерении проводится интегрирование по всем элементарным пучкам составляющим первичный луч, по всем ориентировкам блоков мозаики и участвующему отражении объему образца:

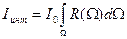(8.1)

Причем

-

свертка аберрационных функций:

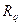- дифракционный профиль, определяемый формфактором;

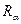- профиль определяемый расходимостью первичного пучка;

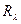- спектральный профиль;

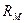- профиль определяемый мозаичностью кристалла;

- профиль профиль определяемый размерами и формой образца;

- аберрационные функции.

Представление конечного профиля в виде свертки отдельных функций позволяет выбрать оптимальные условия измерения .

Графическая интерпретация изменения , основанная на построении Эвальда позволяет выбрать эти условия. Из анализа выражения для статистической ошибки измерений интенсивности и ошибки нестабильности работы прибора:

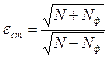
(8.2)

где N и N_ф - общее число импульсов и число импульсов фона,

причем - число импульсов дифракционного пика;

- относительная величина нестабильности измерений.

Следует, что ошибка в измерении фона существенно влияет на результат измерения интенсивности дифракционного пика.

Графическая интерпретация измерений с экваториальной геометрией съемки позволяет выбрать интервал поворота образца и оптимальные размеры апертуры детектора, выяснить оптимальную схему измерени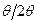й: , или 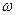- сканирование образца.

На рисунке 8.1 показана графическая интерпретация измерений с помощью представления о конечных размерах узла ОР в пространстве ОР размерностью 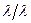=1 - радиус сферы Эвальда. Длины ребер сечения узла плоскостью дифракции связаны с характеристиками условий измерений:

(8.3)

здесь 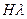- длина вектора ОР ();

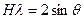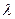- длина волны;

М - угловой интервал разориентации фрагментов образца в освещенном объеме;

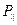- размер освещенного объема образца вдоль линии пересечения дифракционной плоскости с отражающей плоскостью;

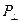- размер рассеивающего объема вдоль нормали к отражающей плоскости;

- спектральный интервал;

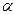- угловая расходимость первичного пучка.

В этой схеме учитывается поворот дифрагированного пучка на угол 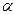и перемещение зоны отражения по кристаллу. Апертура счетчика определяет сканируемый объем в обратном пространстве. Этот объем должен включать в себя весь узел ОР и быть минимальным, чтобы уменьшить вклад фона. Для минимизации сканируемого объема необходимо чтобы его форма и ориентация наилучшим образом соответствовала узлу ОР (рисунок 8.1). Это достигается выбором высоты и ширины щели перед счетчиком (H_c, b_c) и соотношений скоростей вращения образца и счетчика вокруг главной оси гониометра.

Например, при 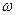- сканировании сканируемый объем - параллепипед, основанием которого является проекция щели счетчика на сферу Эвальда - . Второе слагаемое в форме для отвечает пермещению отражающего объема вдоль нормали к отражающей системе плоскостей. На рисунке 8.2 стрелкой показаны направления движения узла ОР. На рисунках показан также сканируемый объем при таких движениях. Оптимальным будет тот вариант измерения для которого при конкретных условиях эксперимента (угол мозаичности М, расходимость первичного пучка 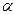и зависящий от угла Брэгга дисперсионный член пропорциональный ). Суммарная интенсивность фона минимальна по отношению к отношению к интенсивности дифракционного пучка. Пользуясь рисунком 8.2 можно выбрать условия эксперимента:

(8.4)

где 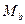- угол мозаичности для разориентировок вокруг горизонтальной оси;

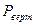и - вертикальная расходимость пучка и размер освещенной области в вертикальном направлении;

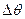- гол поворота кристалла.

2. Определение структуры элементарной ячейки кристаллов.

Определение структуры делится на два этапа. Установление размеров и формы элементарной ячейки, числа структурных единиц в ячейке и симметрии в их расположении. Этот этап называют рентгеновской кристаллографией. Эти сведения получают из анализа геометрии дифракционных картин. Второй этап - рентгеновская кристаллохимия основан на измерении интенсивности дифракционных максимумов - и затем структурного фактора .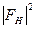

После установления размеров и формы элементарной ячейки, как это было сделано, например, в методе поликристаллов можно найти число структурных единиц N в ячейке:

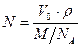(8.5)

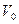где и 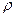- объем ячейки и плотность вещества;

М - молекулярная масса, соответствующая химической формуле вещества в атомных единицах массы;

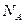- число Авогадро.

Определение отсутствующих отражений или погасаний представляет существенную часть исследования первого этапа, позволяющую установить с той или иной степенью однозначности пространственную группу кристалла.

Если мы зададим какую-либо точку внутри ячейки, то «размножая» ее при помощи совокупности элементов симметрии данной пространственной группы, получим правильную систему точек. Число таких эквивалентных точек называют кратностью правильной системы точек. В каждой пространственной группе существует одна правильная система точек, находящихся в общем положении (вне элементов симметрии), и несколько правильных систем точек в частном положении (на элементах симметрии). Правильные системы точек и соответствуют различным случаям закона расположения атомов в элементарной ячейке.

Очевидно, что в кристалле с примитивной ячейкой структурная амплитуда всегда не равна нулю. Если же ячейка состоит из нескольких эквивалентных по рассеивающей способности атомов или их совокупностей, то при определенной разнице фаз, обусловленной расположением атомов и вектором дифракции, структурная амплитуда может стать равной нулю.

Закономерности погасаний, получающиеся в каждой пространственной группе, можно установить. Для этого нужно принять, что некоторый исходный атом или совокупность атомов занимают в решетке произвольную позицию, и выяснить, какой получается комплекс атомов, если произвести над ними все операции симметрии, соответствующие данной пространственной группе. Полученный комплекс атомов приведет к значениям структурной амплитуды или весовой функции обратной решетки, которые и будут определять закономерности погасаний. Общие закономерности погасаний будут соответствовать обращению в нуль структурной амплитуды при определенных значениях индексов независимо от начальных координат произвольно выбранной исходной частицы.

Закономерности погасания, вызываемые разными элементами симметрии пространственной решетки (систематические погасания) рассмотрены ранее (лекция 5).

Пользуясь интернациональными символами пространственной группы, можно установить законы погасания для этой группы, так как символ содержит знаки решетки Бравэ и открытых элементов симметрии. Однако обратная задача – определение пространственной группы и известных индексов отражений – не всегда решается однозначно, так как одни и те же законы погасания могут встречаться в двух или более пространственных группах.

Если кристалл не огранен и в расположении исследователя нет гониометрических данных, то только по симметрии дифракционных картин нельзя распознать класс симметрии кристалла, а можно установить лишь его дифракционный класс, т.е. в общем случае нельзя определить наличие или отсутствие в кристалле центра симметрии. Погасания же позволяют определить только элементы симметрии второго типа.

Кроме того, существуют пространственные группы с одинаковым набором элементов симметрии, различающихся взаимным расположением и ориентацией. Наконец, имеются 11 пар пространственных групп с идентичным набором и взаимным расположением элементов симметрии, различающихся лишь направлением вращения винтовых осей.

Во всех перечисленных случаях симметрия дифракционных картин и законы погасания не позволяют однозначно отнести данный кристалл к определенной пространственной группе. Существуют 122 рентгенографически различимых случая симметрии, называемых дифракционными группами. Для того чтобы отнести кристалл к той или иной дифракционной группе, сначала проверяют наличие или отсутствие интегральных погасаний, а затем рассматривают, нет ли погасаний зонального или сериального типа. Для определения дифракционной группы можно воспользоваться таблицей дифракционных групп (Миркин Л.И. Справочник по рентгеноструктурному анализу поликристаллов. М., Физматгиз, 1971. 863 с.).

Перейдем теперь к определению атомной структуры кристалла. На этом этапе определяют координаты атомов или распределение электронной плотности в элементарной ячейке кристалла. Для распределения электронной плотности можно записать:

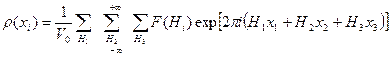(8.6)

где - координата, выражаемая в долях .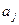

Для выполнения суммирования в выражении (8.6) необходимо знать величину 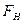, в общем случае комплексную; ее можно записать в виде:

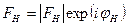(8.7)

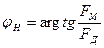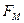где (и 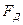- соответственно мнимая и действительная части структурной амплитуды).

Непосредственно из экспериментальных данных можно получить только амплитуды 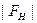, но не их фазы 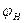. Поэтому приходится находить фазы 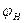структурных амплитуд 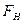с помощью дополнительных искусственных приемов.

Поскольку при известных значениях координат атомов вычислить величины 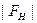и 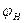не представляет труда, то первым методом решения фазовой проблемы был метод проб и ошибок. На основе данных о симметрии кристалла, о его химическом и молекулярном составе и физических свойствах строят модель структуры, вычисляют значения 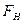и далее сравнивают набор расчетных и экспериментальных значений 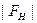. Мерой правильности структуры является так называемый фактор расходимости R:

(8.8)

В современных исследованиях значение 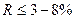обычно считают достаточным для заключения о правильности пробной структуры. При этом следует помнить, что величина 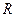может быть небольшой даже при недостаточно точном определении координат атомов. Характерным примером являются кристаллы, содержащие в ячейке наряду с очень легкими тяжелые атомы. В этом случае 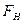мало зависит от положения легких атомов, дающих малый вклад в общую ее величину. Поэтому положение легких атомов находят с большими ошибками. При этом 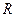-фактор может быть достаточно малым.

На основе ранее предположительно определенной пространственной группы выбирают по интернациональным таблицам правильные системы точек для размещения атомов, учитывая число структурных единиц, приходящихся на одну ячейку. Естественно, что кратность правильных систем точек, на которых размещают атомы разного сорта, должна соответствовать общему числу структурно идентичных атомов данного сорта, приходящихся на одну ячейку (атомы одного элемента, входящие в ячейку в виде ионов с разными зарядами, структурно не идентичны).

В выборе кратности правильных систем точек при размещении ионов руководствуются теорией плотнейших упаковок, учитывая, что каждый анион окружен полиэдром из катионов, причем расстояние анион - катион равно сумме их радиусов. Тип полиэдра определяется тем, что каждый анион стремится окружить себя максимально возможным при заданном соотношении радиусов числом катионов. Если химическая связь в кристалле не чисто ионная, то правила плотнейших упаковок применимы лишь в грубом приближении или совсем неприменимы.

Следует отметить, что центры атомов или ионов могут располагаться на плоскостях, осях или в центре симметрии, а также на таких расстояниях от элементов симметрии, чтобы была возможность реализовать эти преобразования симметрии. Иногда строение кристаллов, особенно в простейших случаях, удается предугадать на основе перечисленных выше принципов.

Рассмотрим распространенный структурный тип флюорита CaF₂. Закономерности погасания для дифракционной картины этого кристалла следующие:

1) индексы отражений общего типа H₁H₂H₃ одинаковой четности, характерное условие для гранецентрированной решетки;

2) для отражений H₁H₂0 H₁ или H₂ всегда четные;

3) отражения типа H00 имеют четные значения H;

4) отражения HHH₃ имеют четную сумму индексов H+H₃.

Таким закономерностям погасания отвечает дифракционная группа m3mF, в которую входят три пространственных группы: Fm3m, F`43m, F432. Отсутствие пьезоэлектрических свойств и огранка кристаллов флюорита свидетельствует о том, что его структурный тип имеет центр симметрии. Это позволяет выбрать единственную группу для флюорита - Fm3m. Сопоставление размера ячейки и плотности позволило вычислить число молекул CaF₂ в одной ячейке, оно оказалось равным 4. Среди координат правильных систем точек группы Fm3m есть частные положения с кратностью 8 и 4: 8(с), 4(а). Очевидно, ионы F могут занимать положение (с), а ионы Ca – (а). Других положений с необходимой кратностью в этой пространственной группе нет. Аналогично для решетки окисной шпинели, содержащей 8 молекул А[B₂]O₄ в ячейке, с пространственной группой Fd3m есть только одно положение правильной системы точек с кратностью 32, где можно разместить атомы кислорода. Кроме того, среди правильных систем точек есть по 2 положения с кратностью 8: (а) и (b) и с кратностью 16: (с) и (d). Если выберем в качестве позиции для А катионов частное положение (а), один из атомов которого имеет координаты 000, то, очевидно, для В катионов необходимо выбирать не (с) положение (один из атомов в этом случае с координатами 1/8 1/8 1/8 будет непосредственным соседом А-катиона), а положение (d). В этом случае анализ интенсивностей необходим лишь для уточнения положения анионов, обладающих одной степенью свободы.

Итак, построенная описанным выше способом приближенная модель нуждается в проверке и уточнении координат атомов, не лежащих в частных положениях. Для этого необходимо сопоставить полученные экспериментально значения |F_H^эксп| со значениями |F_H^расч|, вычисленными на основании пробной модели. При этом желательно знать параметры элементарной ячейки с возможно большей точностью. С помощью дифрактометра углы между осями, для ячеек, в которых они не определены сингонией, можно измерить с точностью до одной угловой минуты, а величины трансляций с точностью 0,005 - 0,01 А. При сопоставлении величин |F_H^эксп| и |F_H^расч| следует учитывать, что значение |F_H ^эксп| уменьшено из-за тепловых колебаний атомов в решетке. Обычно теоретически учесть влияние тепловых колебаний на эффективную величину рассеивающей способности атомов каждого сорта можно лишь весьма приблизительно. Неточное знание величины М_g, тем не менее, означает лишь закономерно растущее с углом дифракции увеличение различия между |F_H^эксп| и |F_H^расч|.

При общем сопоставлении величин |F_H^эксп| и |F_H^расч| эта разница не мещает принципиальной оценке достоверности модели. Однако на заключительной стадии при уточнении коотдинат атомов необходимо добиваться введением температурных поправок сближения |F_H^эксп| и |F_H^расч|. Особенно перспективны измерения интенсивности при низких температурах, в частности при температурах, близких к температуре жидкого азота (78 К), когда влияние тепловых колебаний на интенсивность существенно меньше.

Если при сопоставлении значений |F_H^эксп| и |F_H^расч| совпадения нет, а среди возможных правильных систем точек есть положения, имеющие степени свободы, можно вычислять значения 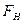как функции координат, определяющих эти степени свободы и проверять, при каком значении параметров наблюдается согласие с экспериментальными значениями |F_H^эксп|. Если координаты типа (х₁х₂х₃) – задача трехпараметрическая. Многопараметрические задачи сводятся иногда к нескольким однопараметрическим, если значения 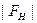для серии разных отражений зависят только от одного параметра. Если же раздельное определение невозможно, то и полное выявление структуры таким методом невозможно.

В современном структурном анализе с успехом используют прямой метод, позволяющий определять межатомные расстояния в ячейке вдоль произвольного направления.

Рассмотрим ряд (8.6), в котором величину r(х¢_j) можно рассматривать как плотность вероятности нахождения электрона в точке с координатами х¢_j. Тогда произведение r(х¢_j) ^. r(х¢_j+x_j) представляет собой плотность вероятности одновременного нахождения одного заряда в точке х¢_j а другого в точке (х¢_j+x_j) на расстоянии 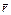от первого (). Функция Паттерсона вводится следующим образом:

(8.9)

Подставив r(х_j) в виде ряда (8.6) в (8.9) и учитывая ортогональность коэффициентов Фурье, получим:

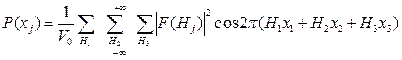(8.10)

Отсюда видно, что ряд Р(x_j) зависит от 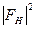, которые могут быть найдены непосредственно из эксперимента.

Электронная плотность в пространстве между атомами близка к нулю, а около центров атомов резко возрастает.

При интегрировании по всему объему ячейки, т.е по всем 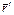, в (8.9) очевидно, что, если вектор 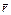не совпадает ни с одним из межатомных отрезков, величина произведения r(х¢_j) ^. r(х¢_j+x_j) повсюду остается малой и значения функции Р(x_j) не велики, но если вектор 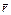равен одному из межатомных расстояний в ячейке, функция будет иметь максимум. Очевидно, что высота максимума зависит от того, какие атомы соединяет отрезок 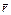. Существенным при вычислении функции является то, что положение максимумов зависит только от расстояния между атомами, т.е. от величины и направления (с точностью до знака) вектора 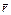, но не зависит от координат атомов соединяемых этим вектором.

Таким образом, значение функции Паттерсона в том, что ее максимумы возникают в точках, которые с хорошей степенью точности соответствуют направлению и величине межатомных расстояний в кристалле, что для расчета не требуется никаких предварительных допущений, так как 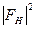могут быть найдены непосредственно измерением интегральных коэффициентов отражения. Вычисление функции Р(x_j) дает непосредственно набор межатомных векторов и является наиболее эффективным методом получения информации для построения пробной структуры.

Реальная точность определения расстояния между центрами тяжести атомов, необходимого как расстояние между двумя максимумами функции Р(x_j), равна 0,01 А. Трудность непосредственного использования набора межатомных векторов состоит в том, что, соединяя максимум функции Р(x_j), расположенный в начале координат, со всеми остальными максимумами, получаем (N² – N)/2 (где N – число атомов в ячейке) независимых векторов. При этом взаимное расположение этих векторов приходится лишь предполагать на основе знания симметрии, координат правильных систем точек, кристаллохимических размеров атомов.

Существенным дополнением, облегчающим построение пробной структуры с помощью функции Р(x_j), является построение так называемых сечений Харкера. Оно состоит в вычислении двумерных сечений трехмерной функции Р(x_j), которые связаны с элементами симметрии кристалла.

Пусть кристалл имеет плоскость симметрии m, перпендикулярную оси . Очевидно, что межатомные векторы в направлении, перпендикулярном плоскости m, равны удвоенной координате x₂. Действительно, каждому атому с координатами 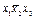сопутствует атом с координатами x₁x₂x₃. Компоненты межатомного вектора равны 0, 2х₂, 0. Построим одномерное «сечение» Р (0х₂0), которое в соответствии с (8.10) можно вычислить из следующего соотношения:

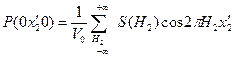(8.11)

где

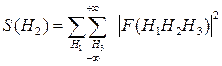
Координата х¢₂ максимумов этой функции равна, очевидно, 2 х₂.

Если плоскость симметрии является скользящей (например, со скольжением вдоль оси а₁), то эквивалентные атомы лежат в точках 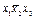и х₁+1/2, х₂, х₃. Тогда построив «сечение»

где

Найдем опять координату х₂ всех атомов в ячейке: 2х₂=х¢₂.

Если в кристалле имеются оси симметрии, то, воспользовавшись тем же приемом, можем построить сечение функции Р(х₁х₂х₃). В частности, для оси 2, параллельной оси решетки а₁, связывающей два тождественных атома с координатами х₁х₂х₃ и 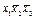можем построить следующее «сечение»

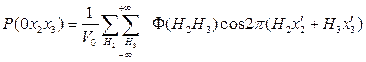
где

Координаты х¢₂х¢₃ максимумов позволяют найти координаты атомов х₂ и х₃ из соотношений х¢₂=2 х₂ и х¢₃=2х₃.

Аналогичные «сечения» можно построить для всех плоскостей и осей симметрии.

В таблице 1 указаны «сечения» функции Р(x_j), используемые для определения координат атомов при наличии в кристалле элементов симметрии.

Таблица 1

Сечение функции Р(x_j), используемые для определения координат

(приведены сечения для элементов симметрии, перпендикулярных оси а₁)

Элементы симметрии	Тип сечения	Плоскость скользящего отражения со скольжением	Тип сечения
2, 3, 4, 42,`4, 6, 63	Р (0 х2 х3)	а2/2	Р (х1 ½ 0)
21, 41, 43, 61, 65	Р (½ х2 х3)	а3/2	Р (х1 0 ½)
31, 32, 62, 64	Р (^1/3 х2 х3)	(а2+а3)/2	Р (х1 ½ ½)
m	Р (х1 0 0)	(а2+а3)/4	Р (х1 ¼ ¼)

Из таблицы видно, что по «сечениям» первого типа находят координаты х₂, х₃; соответственно по «сечениям», связанным с осями симметрии, параллельными другим ребрам элементарной ячейки, можно определить координаты х₁ и х₃ или х₁ и х₂. По сечениям второго типа находят координату х₁, или х₂, или х₃.

Фазу j_H структурной амплитуды легко вычислить с достаточной точностью, если известны координаты атомов. Возможная неточность в знании координат атомов не вызывает значительных ошибок в определении фазы (или знака для кристаллов с центром симметрии), если 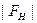не слишком близка к нулю. Абсолютные значения структурных амплитуд находят из экспериментальных измерений интегральных коэффициентов отражения.

При построении распределения электронной плотности следует учесть два обстоятельства:

1. Ряд Фурье в выражении (8.6) содержит бесконечное число членов, тогда как число отражений, а следовательно, и число экспериментально определенных значений 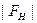всегда ограничено. Поэтому при суммировании приходится обрывать ряд на некотором n-ном члене. Обрыв ряда не вносит существенных искажений, если сумма отброшенных членов достаточно малая величина. Последнее возможно, если амплитуды отбрасываемых членов ряда не превышают 0,03-0,05 от максимальной амплитуды. Следствием обрыва ряда является «расплывание» максимумов электронной плотности по сравнению с истинной их формой. Наиболее последовательным путем устранения искажений в распределении электронной плотности из-за обрыва ряда при суммировании является использование коротковолнового излучения. Благодаря этому существенно увеличивается общее число отражений, а отражения под большими углами q, близкими к 90⁰, будут такими слабыми, что их амплитуда действительно не будет превышать 0,03 от максимальной амплитуды. Поэтому в рентгеноструктурных исследованиях применяют коротковолновые излучения MoK_a (l=0,71 A) или даже AgK_a (l=0,54 A).

2. Надежность данных о распределении электронной плотности зависит от точности измерения интегральных коэффициентов отражения. Дифрактометрические методы измерения интенсивности позволяют определять 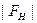с точность 1-4%. Этого достаточно, чтобы можно было в некоторых случаях по картине распределения электронной плотности заметить перераспределение электронов в кристалле, обусловленное химическим взаимодействием между атомами, соседствующими в

элементарной ячейке..

Дата добавления: 2014-01-07