Часть 5. Элементы теории вычислительной сложности

Математическая логика и теория алгоритмов. Курс лекций

В.В. Гуренко

Раздел 2. Теория алгоритмов

(продолжение)

В процессе проектирования и реализации программных и программно-аппаратных систем является обязательным качественное оценивание алгоритма. Критерием оценки качества принято считать сложность алгоритма. Для получения объективной оценки сложность должна иметь количественное выражение.

Можно считать, что два алгоритма А₁ и А₂, применяемые к одному и тому же классу задач, сравнимы по длине кода (например, количеству операторов языка программирования). Чем короче код, тем, казалось бы, алгоритм лучше. Однако можно привести достаточное число примеров, когда короткая программа работает дольше, чем длинная, причем намного.

На практике более приемлема временн á я оценка сложности. Необходимо понимать, что временн ы е оценки не привязывают к техническим характеристикам конкретной вычислительной среды (компьютерной системы).

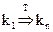Как вариант, можно построить математическую модель алгоритма, например, машину Тьюринга, и число тактов ее работы принять за временн у ю оценку, т.е. сложность алгоритма. Число тактов ТМ равно количеству конфигураций тьюрингова вычисления, приводящего к преобразованию исходного слова a на ленте к результирующему слову β = Т(a).

Однако построение ТМ может оказаться процессом громоздким и сложным. Поэтому считают, что алгоритм реализуется на некоторой абстрактной машине, которая каждый шаг алгоритма выполняет за одну единицу времени. За шаг алгоритма принимают, соответственно, одну операцию: действие по обработке данных (например, сложение, умножение, адресация операнда, пересылка), операцию ввода/вывода, операцию ветвления, вызов процедуры и т.д. Единица времени в конкретных величинах никак не измеряется. Таким образом, сложность двух алгоритмов сравнима по затраченным ими количествам единиц времени.

Характеристикой временн о й сложности является также число обращений к памяти. Понятно, что число обращений к памяти и объем памяти, требуемый для реализации алгоритма, – разные параметры, характеризующие алгоритм. Первый отражает временн у ю характеристику алгоритмической сложности, второй позволяет оценивать так называемую пространственную (емкостную) алгоритмическую сложность.

В случае ТМ число ячеек на ленте, к которым обращалась машина для чтения/записи в процессе работы над исходным словом a отражает временн у ю сложность алгоритма, а в целом количество ячеек ленты, необходимое для работы ТМ на данном слове, отражает пространственную сложность. Понятно, что и временная, и пространственная сложность алгоритма зависит от размерности исходных данных, к которым он применяется. Очевидно, однако, что размерность данных гораздо больше влияет на временн у ю сложность.

Так, в случае поиска кратчайшего пути в графе классические алгоритмы Форда и Дейкстры будут менее эффективными с точки зрения затрачиваемых единиц времени, чем метод полного перебора, если число вершин графа 5–6, и более эффективными на графах с числом вершин 10-15. Сами алгоритмы Форда и Дейкстры на больших графах имеют разную временн у ю сложность: чем выше мощность множества вершин, тем более эффективен алгоритм Дейкстры и менее эффективен алгоритм Форда.

В теории алгоритмов принято выполнять построение функции от размерности задачи именно для определения временн о й сложности алгоритма, и в дальнейшем, говоря о сложности алгоритма, будем подразумевать именно временн у ю сложность. Саму функцию будем называть функцией сложности. В частности, сложность алгоритмов на графах можно рассматривать как функцию сложности от числа вершин графа. Функцию необходимо строить для худшего случая, т.е. наименее благоприятного с точки зрения объема вычислений в ходе решения задачи.

В принято разделять алгоритмы на два класса в зависимости от характера функции сложности.

1). Полиномиальные, или «хорошие» алгоритмы. Функция сложности «хорошего» алгоритма представима в виде некоторого полинома. Например:

T(n) = 15n³ + 2n² + 3n – 7,

где n – размерность задачи (в частности, число вершин графа).

2). Экспоненциальные, или «плохие» алгоритмы. Функция сложности такого алгоритма не представима полиномом. Их называют экспоненциальными несмотря на различный математический характер. Например, функция сложности может иметь в своей записи вычисление факториала и не содержать вычисление экспоненты. Однако любая неполиномиальная функция сложности представима в виде:

T(n) = 2^P(n),

где P – некоторый полином.

Полиномиальный алгоритм считают приемлемым, если степень полинома не более 4.

В построении точной функции сложности нет необходимости, т.к. с увеличением размерности задачи влияние коэффициентов при меньших степенях полинома и самих младших степеней становится незначительным. На практике оказывается достаточным оценить рост функции сложности с увеличением размерности задачи. Это достигается при помощи асимптотической оценки функции сложности.

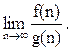Смысл заключается в сравнении некоторой реальной функции f(n) и идеальной (упрощенной) функции g(n) при n ® ¥:

Если этот предел есть const > 0, то говорят, что f(n) = O(g(n)) (читается «О большое от g от n).

Например, для приведенного выше полинома можно записать:

f(n) = 15n³ + 2n² + 3n – 7,

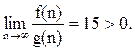g(n) = n³,

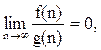Если то говорят, что f(n) = о(g(n)) (читается «О малое от g от n).

В предыдущем примере можно положить g(n) = n^3,5, т.к.

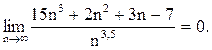Тогда f(n) = o(n^3,5).

O(g(n)) называют верхней границей функции сложности, а

o(g(n)) называют нижней границей функции сложности.

Когда это возможно, стремятся к получению верхней границы, т.к. время работы алгоритма растет с увеличением размерности задачи n не быстрее, чем g(n).

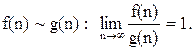Говорят, что реальная функция сложности f(n) асимптотически эквивалентна идеальной функции сложности g(n), если указанный предел равен единице:

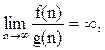Если верхней границы функции сложности не существует, т.е. то
пишут: f(n) = Ω(g(n)) (читается «Омега большое от g от n).

Дата добавления: 2014-01-07