
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вынужденные электрические колебания. Резонанс колебаний
|
|
|
|
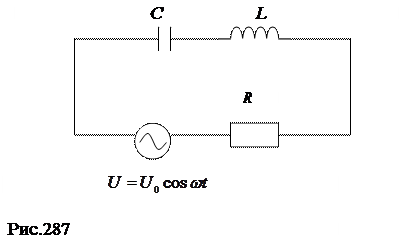
Чтобы реальные электрические колебания совершались длительное время, необходимо систему (контур) подпитывать энергией. Если в контур включим источник, вырабатывающий периодически изменяющееся напряжение, то в системе (рис.287) будут совершаться вынужденные электрические колебания. Пусть внешнее напряжение в контуре изменяется по закону:
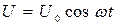 . .
| (672) |
Найдем изменения силы тока, напряжения, заряда. Для этого используем второе правило Кирхгофа: 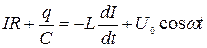 (673)
(673)
или 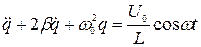 , (674)
, (674)
где
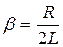 ; ; 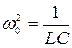 . .
| (675) |
Решение дифференциального уравнения (674) ищем в виде:
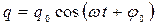 , ,
| (676) |
| Берем производные от (676): | |
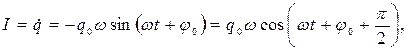
| (677) |
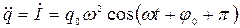 . .
| (678) |
Обозначим сдвиг фаз через 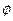 :
:
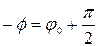 или или 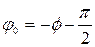 . .
|
Тогда выражения (676) – (678) запишутся в виде:
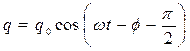 , ,
| (679) |
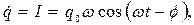 , ,
| (680) |
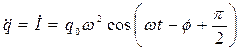 . .
| (681) |
Подставляя выражения (679) - (681) в (674), получим:
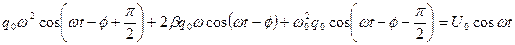 . .
| (682) |
Используем метод векторной диаграммы, представляя коэффициенты при cos в виде векторов:
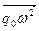 , , 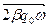 , , 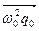 , , 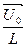 . .
|
Тогда в системе координат XY эти векторы можно представить в виде (рис.288).
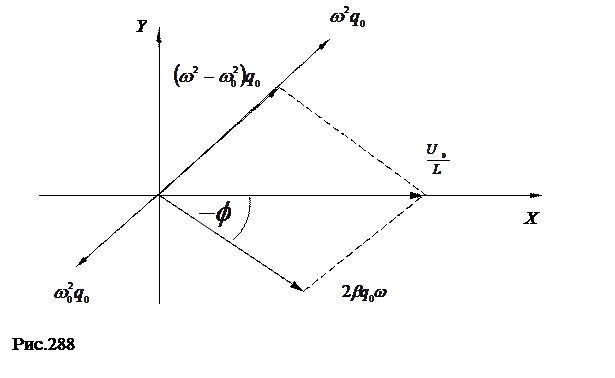
Из рис.288 найдем:
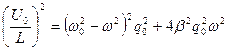 , ,
|
тогда амплитуда заряда на конденсаторе равна:
 . .
| (683) |
Сдвиг фаз:
 , ,
| (684) |
| и начальная фаза колебаний: | |
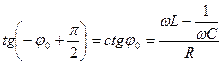
| |
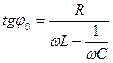 . .
| (685) |
Представим (683) в виде:

| (686) |
Сила тока, напряжение в цепи изменяются по закону:
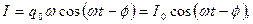
| (687) |
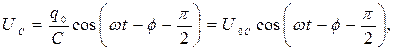
| |
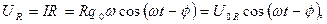
| |
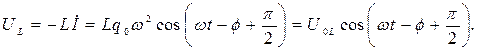
|
На декартовой системе координат (X, Y) отложим амплитудные значения всех напряжений, и получим диаграмму, представленную на рис.289.
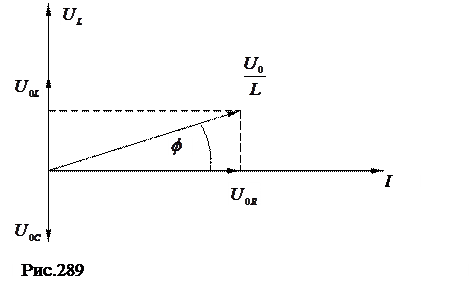

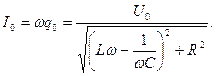
| (688) |
С учетом (686), амплитудное значение силы тока в цепи равно
Амплитуда напряжения на конденсаторе
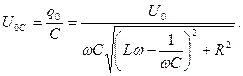
| (689) |
Амплитудное значение ЭДС на катушке
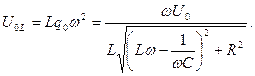
| (690) |
Исследуем амплитуды 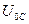 и
и 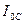 .
.
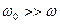 , то , то
| 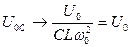 , ,
|
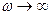 , то , то
| 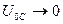 , ,
|
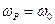 , то , то
| 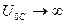 ; ;
|
 Для
Для 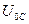 :
:
1) пусть 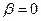 и если:
и если:
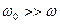 , то , то
| 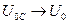 , ,
| |
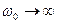 , то , то
| 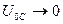 , ,
| |
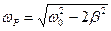 , то , то
| 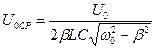 . .
| (691) |
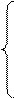
2) пусть 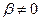 и если:
и если:
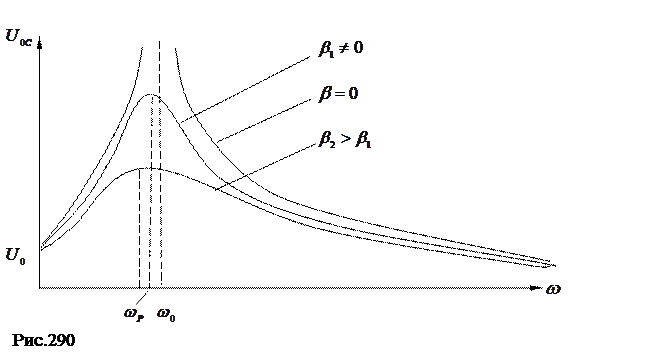
Таким образом, при частоте
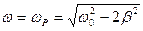
| (692) |
наблюдается резонанс (резкое усиление амплитуды колебаний) 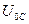 (рис.290).
(рис.290).
Для амплитуды силы тока:
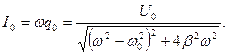
|
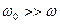 , то , то
| 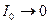 , ,
| |
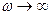 , то , то
| 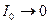 , ,
| |
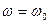 , то , то
| 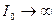 ; ;
|
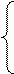
1) пусть 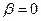 и если:
и если:
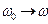 , то , то
| 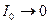 , ,
| |
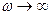 , то , то
| 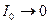 , ,
| |
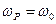 , то , то
| 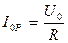 . .
| (693) |
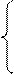
2) пусть 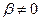 и если:
и если:
При 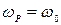 наступает резонанс силы тока
наступает резонанс силы тока
На рис.291 дана зависимость  от
от 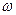 .
.
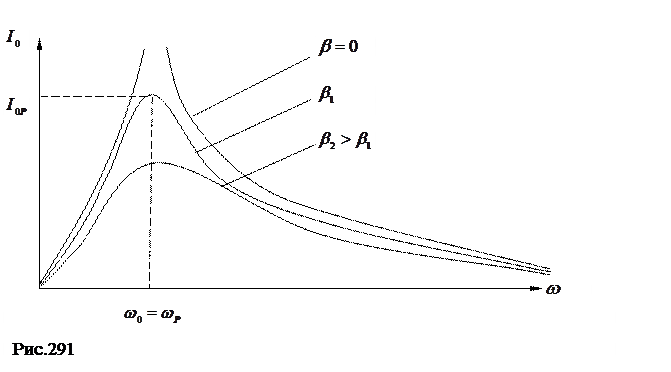
Рассмотрим, как связана добротность системы с частотой колебаний при малых затуханиях, т.е. 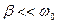 . Для этого исследуем зависимость амплитудных значений силы тока от частоты (рис.292).
. Для этого исследуем зависимость амплитудных значений силы тока от частоты (рис.292).
В технике за ширину рабочей частоты 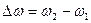 принимается разность частот
принимается разность частот 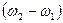 , соответствующих 0,7 резонансного значения силы тока, т.е.
, соответствующих 0,7 резонансного значения силы тока, т.е. 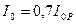 . Тогда с учетом (688) и (693) получим
. Тогда с учетом (688) и (693) получим
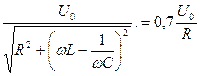 . .
| (694) |
Возведем выражение (694) в квадрат и, учитывая, что 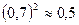 , получим
, получим
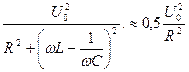 или или 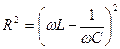 . .
| (695) |
Решаем уравнение (695), и, отбрасывая отрицательные корни, получим:
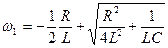 и и  . .
| (696) |
Тогда
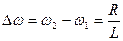 . .
| (697) |
Найдем отношение
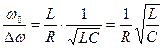 . .
| (698) |

Сравним с выражением (670) и получим, что
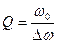 . .
| (699) |
Из соотношения (699) видно, что если 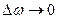 , то
, то 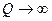 и наоборот. Это значит, что при
и наоборот. Это значит, что при 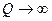 потеря энергии системы практически равна нулю, что замечательно! Однако
потеря энергии системы практически равна нулю, что замечательно! Однако 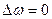 означает, что форма сигнала острая и точно фиксировать (удержать) сигнал невозможно. Если
означает, что форма сигнала острая и точно фиксировать (удержать) сигнал невозможно. Если 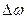 велика, то вероятность фиксировать сигнал велика, но уменьшается добротность
велика, то вероятность фиксировать сигнал велика, но уменьшается добротность 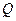 , т.е. система работает с очень большой потерей энергии, что нежелательно. Поэтому формула (699) определяет оптимальный вариант работы системы, при котором система фиксирует стабильный сигнал при минимальной потере энергии. Формула (699) используется при конструировании радиотехнических систем.
, т.е. система работает с очень большой потерей энергии, что нежелательно. Поэтому формула (699) определяет оптимальный вариант работы системы, при котором система фиксирует стабильный сигнал при минимальной потере энергии. Формула (699) используется при конструировании радиотехнических систем.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 533; Нарушение авторских прав?; Мы поможем в написании вашей работы!