Формулировка и решение задачи

Введем обозначения:

С ₁ – затраты на создание запаса на [0, θ],

C ₂ – затраты на хранение запаса на [0, θ].

Тогда суммарные затраты на [0, θ] будут:

С = С ₁ + С ₂.

σ₁ – затраты на доставку 1 партии заказа (не зависит от размера партии).

σ₂ – затраты на хранение 1 единицы заказа в 1 единицу времени.

Найдем число заказываемых партий:

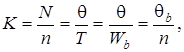
где N – суммарная потребность комплектующих (материалов).

Замечание. Объем заказа n должен быть таким, чтобы число заказов партий было целым, то есть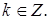

Найдем компоненты суммарных затрат:

1. Затраты на создание запаса.

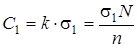на [0, θ].

2. Затраты на хранение запаса.

Рассмотрим затраты на хранение запаса на [0, T ]. Найдем затраты на хранение имеющегося запаса в 1 единицу времени. Это

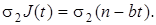
Суммарные затраты на [0, T ] получаются следующим образом:

Суммарные затраты на хранение запасов на [0, θ] равны

Итак, функция суммарных затрат:

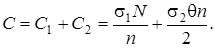
Математически задача оптимального управления запасами записывается так:

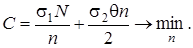
Замечание. В действительности затраты на доставку заказа обычно зависят от объема партий, например, линейно, поэтому для учета этих затрат введем обозначение:

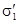- затраты на доставку 1 единицы заказываемой продукции. Тогда затраты на доставку одной партии объема n будут 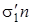. Суммарные затраты получатся путем умножения на число партий: 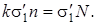В этом случае функция затрат будет иметь вид:

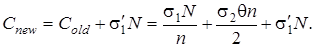
То есть добавляется в старую функцию затрат некоторая const.

2. 1. 2. Формула Вильсона (Уилсона)

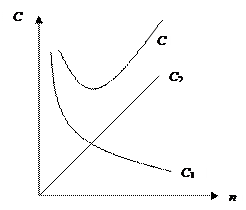
График функции затрат 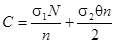имеет вид:

Оптимальное значение n найдем следующим образом. Вычислим производную и приравняем к 0:

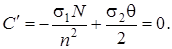
Из этого уравнения следует, что

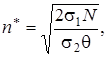
где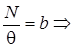

   

(*)

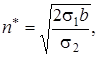
Определение. Формула (*) называется формулой Вильсона (Уилсона) или формулой наиболее экономичного объема партии.

Замечание. Решение оптимизационной задачи должно учитывать условие

,

если 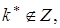то на практике изменяют n^* до величины n^** так, чтобы

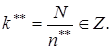
Полагаем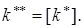

Окончательный объем партии будет таким:

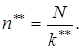
Анализ решения задачи

Из уравнения 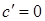имеем равенство

,

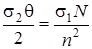умножив которое на n, получим:

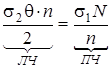
ЛЧ – затраты на хранение запасов;

ПЧ – затраты на пополнение запасов.

То есть оптимальный объем партии определяется точкой пересечения графиков функций затрат С ₁ и С ₂.

Вывод: минимальное значение суммарных затрат в рассматриваемой задаче оптимального управления запасами достигается, когда затраты на создание запаса на [0, θ] равны затратам на хранение запаса на [0, θ].

Оптимальные суммарные затраты

Рассмотрим функцию затрат:

.

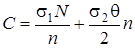Так как в точке оптимума слагаемые должны быть равны, то минимальные затраты:

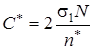(а)

или

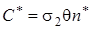(б)

Рассмотрим (а), где используем формулу Вильсона для n^*:

.

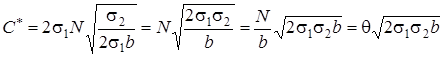Аналогично имеем из равенства (б):

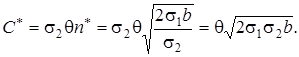
Учитывая, что 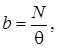получим

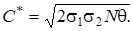
Число оптимальных партий

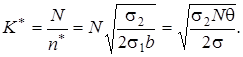
Замечание: Если 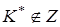, то 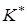можно подкорректировать так:

.

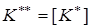Время расходования оптимальных партий

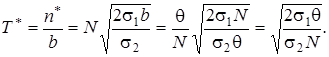
Пример: Имеется сборочный цех, потребность которого составляет 120 000 деталей в год. Они расходуются равномерно и непрерывно во времени. Заказываемые партии деталей поступают через равные промежутки времени. Хранение одной детали на складе стоит 0,35 рублей в сутки. Поставка одной партии деталей стоит 10 000 рублей. Требуется найти наиболее экономичный объем партии n^* и интервал между поставками T^*.

Решение. Исходные данные σ₁ = 10 000 руб., σ₂ = 0,35 руб., θ = 365 дней, N = 120 000 деталей. Оптимальный объем партии по формуле Вильсона:

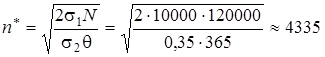деталей.

Тогда

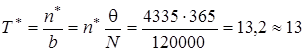дней.

Замечания. В условиях реального производства обычно объем партии несколько завышают и выражают в «круглых цифрах». В рассмотренной задаче можно взять n^* = 4500. В этом случае T^* тоже изменится (возрастет). Возникает вопрос: насколько при этом увеличится величина суммарных затрат на поставку и хранение заказа?

Дата добавления: 2014-01-07