Бифуркационные диаграммыи модельные системы

О содержании данной брошюры

Цель настоящей работы состоит в том, чтобы дать представление о некоторой совокупности результатов, полученных на сегодняшний день в рамках сформулированной исследовательской программы. Обсуждаются динамические системы на прямой и на плоскости, т. е. одно дифференциальное уравнение и система двух дифференциальных уравне­ний, зависящие от параметров. Описываются бифуркационные диаграммы и фазовые портреты для бифуркаций, встречающихся в системах с одним, двумя и тремя параметрами.

Основное внимание в работе уделяется бифуркациям положений равновесия (мы называем такие бифуркации локальными). В меньшей степени, но, по существу, тоже достаточно подробно обсуждаются бифуркации предельных циклов и сепаратрис (так называемые нелокальные бифуркации). Дело в том, что бифуркационные диаграммы в окрестности точек, отвечающих бифуркациям положений равновесия, могут содержать границы, на которых происходят бифуркации предельных циклов и сепаратрис. Иначе говоря, бифуркации положений равновесия в ряде случаев сопровождаются также бифуркациями предельных циклов и сепаратрис, описание таких нелокальных бифуркаций с необходимостью включается в описание локальных. (Отмеченное обстоятельство, создающее значительные трудности в работе «теоретика», является весьма удачным для «прикладника», поскольку позволяет обнаруживать нелокальные бифуркации посредством исследования локальных.)

Изложение сведений о бифуркациях положений равновесия в системах на плоскости является достаточно полным. Большинство представленных результатов получены аналитически; описание одной из наиболее «трудных» бифуркаций основано на результатах аналитических исследований и численного моделирования

При описании бифуркаций мы пользуемся такими понятиями, как коразмерность бифуркации, условия вырождения и невырожденности, модельная система и др. Все эти понятия подробно обсуждаются в гл. 2. В гл. 3 описываются бифуркации положений равновесия в системах с одной динамической переменной. В ней в наиболее простом виде иллюстрируется метод последовательного рассмотрения все более сложных бифуркаций. Этот метод применяется затем в гл. 4 к изучению динамических систем с двумя переменными.

Хотя в данной работе подробно рассматриваются бифуркации лишь в си­стемах с одной и двумя динамическими переменными, важно подчеркнуть, что те же бифуркации встречаются в много­мерных системах и являются типичными для них, наряду с другими, собственно «многомерными» бифуркациями. Описа­ние этих одно- и двумерных бифуркаций естественно обобщается на многомерный случай с помощью идеи центрального многообразия и принципа сведения. Этому вопросу посвящена гл. 5.

В заключительных замечаниях приводится список рассмотренных бифуркаций и обсуждается схема применения изложенных теоретических результатов к анализу конкретных систем дифференциальных уравнений. Везде в тексте мы стараемся иллюстрировать общее описа­ние бифуркаций примерами, когда эти бифуркации встречаются в конкретных моделях.

В данной работе рассматриваются лишь так называемые системы общего положения, т. е. системы, на которые не наложены никакие специальные ограничения типа условий равенства. В системах, имеющих группы симметрии, консервативных и других системах «не общего положения», часто встречающихся в приложениях, возникают другие бифуркации, отличные от тех, что описаны в данной брошюре. Пример — потеря устойчивости положения равновесия в системе, обладающей симметрией отра­жения, приводящая к ответвлению от него двух новых устойчивых положений равновесия (так называемая вилка). Бифуркации такого рода называют несовершенными. Обзор бифуркаций для различных классов систем не общего положения — интересная самостоятель­ная тема.

Рассмотрим систему дифференциаль­ных уравнений

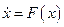(2.1)

где 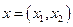—фазовые переменные, —функции, имеющие достаточное число производных (как говорят, достаточно «гладкие»). Задача качественного исследования системы (2.1) состоит в установлении топологии ее фазового портрета. При этом два фазовых портрета считаются топологически эквивалентными, если существует гомеоморфизм (взаимно-однозначное непрерывное отображение), переводя­щий один фазовый портрет в другой с сохранением направления движения по траекториям. В частности, на топологически эквивалентных фазовых портретах число положений равновесия и предельных циклов одинаково. Одинаковы также характер устойчивости соответствующих циклов и равновесий, их взаимное расположение.

Топология фазового портрета грубой системы не меняется при любых достаточно малых изменениях этой системы. Как уже отмечалось выше, в грубой системе положения равновесия не имеют мультипликаторов, равных единице, и отсутствуют сепаратрисы седел, образующие петлю или идущие из одного седла в другое.

Напротив, фазовый портрет негрубой системы при некотором ее малом изменении становится топологически неэквивалентным исходному (испытывает бифуркацию). Например, на фазовом портрете меняется число положений равновесия или их устойчивость. Как правило, бифуркации происходят в окрестности особых траекторий — положений равновесия, предельных циклов, сепаратрис. Назовем бифуркацию локальной, если она происходит в сколь угодно малой, но фиксированной окрестности некоторо­го положения равновесия системы (2.1). Все остальные бифуркации в настоящей работе называются нелокальными. Примером локальной бифуркации является рождение из фокуса малого предельного цикла (бифуркация Андронова — Хопфа), примером нелокальной — рождение предельного цикла из петли сепаратрисы седла.

Пусть теперь имеется система диффе­ренциальных уравнений, зависящая от параметров:

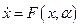, (2.2)

где 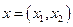—фазовые переменные, — параметры. Будем предполагать, что система (2.2) является системой общего положения, т. е. не удовлетворяет никаким специальным условиям типа равенства.

Грубая система заполняет область в пространстве параметров (2.2). Во всех точках такой области фазовые портреты системы топологически эквивалентны. Точки пространства параметров, отвечающие негрубым системам, называются бифуркационными точками. Фазовый портрет в их окрестности испытывает бифуркации.

Окрестность данной бифуркационной точки в пространстве параметров системы (2.2) разбивается на связные множества, отвечающие топологически экви­валентным фазовым портретам в неко­торой фиксированной области фазовой плоскости. Это разбиение образует бифуркационную диаграмму. Задача качественного исследования системы (2.2) в окрестности бифуркационной точки состоит в описании ее бифуркационной диаграммы и соответствующих фазовых портретов.

Описание бифуркационных диаграмм и фазовых портретов проводится с точностью до топологической эквивалентности диаграмм. Две бифуркационные диаграммы (вместе с соответствующими им фазовыми портретами) мы называем топологически эквивалентными, если существует гомеоморфизм параметри­ческих окрестностей бифуркационных точек, переводящий одну диаграмму в другую, и при этом такой, что фазовые портреты в соответствующих параметрических точках двух диаграмм топологически эквивалентны.

Замечание. Описанную эквивалентность бифуркационных диаграмм можно назвать послойной, или слабой эквивалентностью. Часто дополнительно в определение эквивалентности включают

требование непрерывной параметрической зависимости гомеоморфизма, уста­навливающего эквивалентность фазовых портретов в соответствующих параметрических точках.

Будем говорить, что данной бифуркационной точке отвечает бифуркация коразмерности k, если в ней выполняются k бифуркационных условий (условия типа равенства) и некоторый набор условий невырожденности (условия типа неравенства). Бифуркационные условия выделяют в пространстве параметров бифуркационную поверхность (многообразие) коразмерности k. При нарушении бифуркационных условий, т. е. при сдвиге с этого многообразия, система (2.2), как правило, становится грубой, а если и остается негрубой, то топология ее бифуркационной диаграммы изменяется. Условия невырожденности гарантируют, что данная точка на бифуркационном многообразии не попадает на подмногообразие, отвечающее бифуркации более высокой коразмерности.

Например, бифуркация Андронова — Хопфа имеет коразмерность 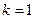и задается одним бифуркационным условием 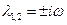, где 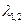— собственные числа положения равновесия. В системе (2.2) это условие выделяет бифуркационное многообразие коразмерности один (размерности m —1). При пересечении этого многообразия рассматриваемое положе­ние равновесия превращается из устойчивого фокуса в неустойчивый. Условием невырожденности для бифуркации Андронова — Хопфа является неравенство 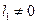, где величина 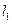— первая ляпуновская величина — составлена по определенному правилу из производных до третьего порядка включительно от правых частей системы (2.2) в положении равновесия. При 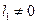пересечение параметрической точкой бифуркационного многообразия сопровождается рожде­нием единственного малого предельного цикла. Одновременное выполнение ус­ловий 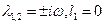задает многообразие коразмерности два на рассматриваемом бифуркационном многообразии. Оно отвечает бифуркационным точкам коразмерности два и выше; в окрестности типичных точек этого множества возможно рождение из равновесия не одного, а двух предельных циклов.

Чтобы полностью описать бифуркацию, заданную набором бифуркационных условий и условий невырожденности, необходимо указать для нее все топологически различные бифуркационные диаграммы, описать перестройки фазо­вых портретов и сформулировать усло­вия, при которых реализуется каждая из диаграмм. Обычно классы эквивалентных между собой диаграмм выделяются как области знакопостоянства функций, задающих условия невырожденности. Это означает, что каждой области на бифуркационном многообразии, выделяемой условиями невырожденности, отвечает одна бифуркационная диаграмма. В разных областях бифуркационные диаграммы могут быть одинаковыми или различными. В случае бифуркации Андронова — Хопфа при 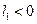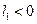потеря устойчивости фокуса сопровождается рождением из него малого устойчивого предельного цикла. При 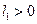, напротив, потеря устойчивости фокуса связана с «гибелью» на нем неустойчивого предельного цикла. Таким образом, здесь имеются два топологически неэквивалентных типа бифуркационных диаграмм, отвечающих «мягкой» (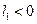) и «жесткой» (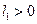) потере устойчивости фокуса. Об этом подробнее будет сказано далее.

Далее будут последовательно описаны все локальные бифуркации коразмерности один, два и три. При этом бифуркация следующей коразмерности будет возникать в результате превращения некоторого условия невырожденности для бифуркации предыдущей коразмерности в новое бифуркационное условие. Мы рассмотрим и нелокальные бифуркации коразмерности один и два, с необходимостью возникающие в окрестности бифуркационных точек локальных бифуркаций коразмерности два и три. Эти бифуркации будут описываться в порядке их появления

Для всех рассматриваемых ниже локальных бифуркаций бифуркационные условия и условия невырожденности формулируются через конечный набор производных от правых частей системы, вычисленных в положении равновесия. Для каждой из этих бифуркаций удается построить зависящую от параметров полиномиальную систему, удовлетворя­ющую необходимым бифуркационным условиям и условиям невырожденности и обладающую тем свойством, что в ней реализуются все возможные для данной бифуркации бифуркационные диаграммы. Такую систему мы называем далее модельной. Модельная система для бифуркации Андронова — Хопфа в полярной системе координат 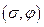имеет вид:

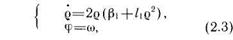
где 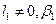— бифуркационный параметр.

Основным определяющим свойством модельной системы является то, что любую систему в фазово-параметрической окрестности локальной бифуркации можно привести к соответствующей модельной системе в следующем смысле. Сначала с помощью замен переменных, параметров и времени система приводится к модельной системе с точностью до членов некоторого порядка. Затем члены более высокого порядка, не влияющие на топологию бифуркационных диаграмм, отбрасываются. Из процедуры приведения следует, что бифуркационная диаграмма и фазовые портреты в исходной системе могут быть получены (с точностью до топологической эквивалентности) из бифуркационной диаграммы и фазовых портретов модельной системы.

Мы предполагаем, что приводящие замены непрерывно зависят от парамет­ров системы, так что коэффициенты и параметры в правых частях модельной системы являются непрерывными функциями исходных параметров. Это позволяет рассматривать непрерывное изменение коэффициентов модельных систем при движении по бифуркационному многообразию и формулировать бифуркационные условия и условия невырожденности в терминах модельной системы.

Замечание 1. Модельные системы, коэффициенты которых с помощью дополнительного масштабирования приведены к некоторым стандартным значениям, называются главными деформациями, или главными семействами.

Замечание 2. Полное описание бифуркаций составляет содержание ма-

тематических теорем о топологической версальности. Для некоторых из рассматриваемых ниже случаев теоремы о версальности пока в полной мере не дока­заны.

Замечание 3. При описании нелокальных бифуркаций вместо модельных систем дифференциальных уравнений обычно используются динамические системы с дискретным временем, задаваемые с помощью модельных отображений.

Дата добавления: 2014-01-07