Критерий инверсий

Рассмотрим последовательность N значений слу­чайной величины x(k). Обозначим эти значения символом x_i, где i == 1, 2, 3,..., N.

Подсчитаем теперь число случаев, когда x_i > x_j, при i < j. Каждое такое неравенство называется инверсией. Общее число инверсий обозначается символом А, которое формально определяется так.

По ряду значений x₁, x₂ …, x_N определим величину

.

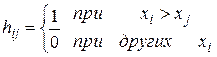Тогда где

Например,

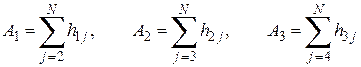и т.д.

Для примера рас­смотрим последовательность N = 8 значе­ний: x₁=5, x₂=3, x₃=8, x₄=9, x₅=4, x₆=1, x₇=7, x₈=5. В этой последовательности x₁ > x₂, x₁ > x₅ и
x₁ > x₆, откуда находим А₁ = 3 инверсиям для x₁. Сопоставляя значение x₂ с последующими значениями ряда (т. е. при i = 2 и i < j = 3, 4,..., 8), можно найти, что x₂ > x₆ и только. Поэтому число инверсий для x₂ составляет A₂ = 1. Продол­жая анализ, можно видеть, что A₃ = 4, A₄ = 4, A₅ = 1, A₆ = 0, A₇ = 1. Общее число инверсий составит A = A₁ + A₂ + … + A₇ = 3+1+4+4+1+0+1 = 14.

Если последовательность N наблюдений содержит независимые значения одной и той же случайной величины, то число инверсий есть случайная величина А(k) со средним значением

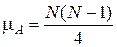
и дисперсией

В приложении 2 содержатся данные о 100a-процентных точках функции распределения величины А(k).

Критерий инверсий вообще говоря, имеет большую мощность, чем критерий серий, при выявлении монотонного тренда в последователь­ности наблюдений. Однако критерий инверсий обладает малой мощностью при выявлении колебательного тренда.

Например, проверим последовательность N = 20 значений, рассмотренных ранее, на наличие тренда при уровне зна­чимости a = 0,05. Число инверсий в этом случае таково:

А1

А2

А3

А4

А5

А6

А7

А8

А9

А10

А11

А12

А13

А14

А15

А16

А17

А18

А19

Общее число инверсий А = 62.

Рассмотрим гипотезу о том, что наблюдения представляют неза­висимые значения случайной величины х(k), не содер­жащей тренда. Область принятия гипотезы определяется неравенством A_{20; 1-a/2} < A £ A_{20; a/2}. По данным приложения 2 при a = 0,05 находим A_20;1-a/2=A_20;0,975 = 64 и A_20;a/2=A_20;0,025= 125.

Следовательно, гипотезу отвергают при 5%-ном уровне значимости, так как значение А = 62 не попадает в интервал между 64 и 125.

Заметим, что гипотеза о независимости этой же последовательности значений при использовании критерия серий была принята. Этот факт иллюстрирует разницу в чувствительности двух методов проверки.

Таблица 11 – Таблица исходных данных и расчетных показателей динамического ряда

(изменения стоимости зернокомбайна «Дон 1500» во времени)

Время T	Цена Р, руб	D баз= Yi-Yo	D цеп= Yi -Yi-1	Кр баз =Yi/Yo	Tр баз= 100*Yi/Yo	Кр цеп= Yi/Yi-1	Tр цеп= 100*Yi/Yi-1	Кпр.баз= Кр.баз-1	Tпр баз= 100*Кр. цеп	Кпр цеп= Кр цеп-1	Тпр цеп= Кпр цеп*100	А цеп= Yi-1/100
1995 1п/г		-	-	0,66	66,34			-0,337	-33,659			-
1995 2п/г		-95260		0,75	74,72	1,13	112,63	-0,25	-25,28	0,13	12,63
1996 1п/г		-25030		0,93	93,36	1,25	124,94	-0,07	-6,64	0,25	24,94	2815,8
1996 2п/г				1,00	100,00	1,07	107,11	0,00	0,00	0,07	7,11	3518,1
1997 1п/г				1,08	107,74	1,08	107,74	0,08	7,74	0,08	7,74	3768,4
1997 2п/г				1,12	111,72	1,04	103,70	0,12	11,72	0,04	3,70	4059,9
1998 1п/г				1,25	124,72	1,12	111,64	0,25	24,72	0,12	11,64
1998 2п/г				1,41	140,78	1,13	112,87	0,41	40,78	0,13	12,87
1999 1п/г				1,72	172,49	1,23	122,53	0,72	72,49	0,23	22,53
1999 2п/г				2,23	223,17	1,29	129,38	1,23	123,17	0,29	29,38
2000 1п/г				2,93	293,00	1,31	131,29	1,93	193,00	0,31	31,29
2000 2п/г				3,50	350,39	1,20	119,59	2,50	250,39	0,20	19,59
2001 1п/г				4,06	405,74	1,16	115,80	3,06	305,74	0,16	15,80
2001 2п/г				4,78	477,92	1,18	117,79	3,78	377,92	0,18	17,79

3.5. Средние показатели рядов динамики

Средние показателирядов динамики являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.

Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.

В интервальном ряду динамики с равноотстоящими уровнями во времени расчет среднего уровня ряда производиться по формуле средней арифметической простой:

.

Средний уровень ряда для цены зернокомбайна по исходным данным

составляет:

Рср = 10333219/15=688881,26 руб

Если интервальный ряд динамики имеет не равноотстоящие уровни, то средний уровень ряда вычисляется по формуле

,

где t – число периодов времени, в течение которых уровень не изменяется.

Для моментального ряда с равноотстоящими уровнями средняя хронологическая рассчитывается по формуле

,

где n – число уровней ряда.

Средняя хронологическая для неравноотстоящих уровней моментного ряда динамики вычисляется по формуле

.

Определение среднего абсолютного прироста производится по цепным абсолютным приростам по формуле:

или .

Средний абсолютный прирост для цены комбайна «Дон 1500» составляет

85322,34/14=6094,5 руб

Среднегодовой темп роста вычисляется по формуле средней геометрической:

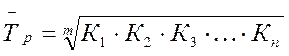, или

,

где m – число коэффициентов роста.

Среднегодовой темп роста для зернокомбайна составляет:

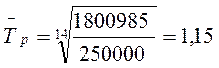
Среднегодовой темп прироста получим, вычтя из среднего темпа роста 100%.

Среднегодовой темп прироста для зернокомбайна «Дон 1500» составляет 15 %.

Дата добавления: 2014-01-07