Бифуркация коразмерности один — двукратное равновесие

Пусть при некоторых значениях параметров собственное число у положения равновесия 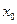обращается в нуль:

,

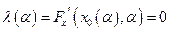но выполняется условие невырожденности: . Тогда — двукратный корень уравнения (3.2). Модельная система для данной бифуркации коразмерности один зависит от одного параметра и имеет вид:

, (3.5)

где

Бифуркационные диаграммы системы (3.5) эквивалентны для всех . Пусть а>0 (этого всегда можно добиться заменой ). Тогда при в системе (3.5) имеются два положения равновесия — устойчивое и неустойчивое (при этом неустойчивое является границей области притяжения устойчивого равновесия). При (они сливаются в полуустойчивое равновесие — возникает негрубая система. При равновесия исчезают (рис. 3.2).

Рис. 3.2 Бифуркационная диаграмма и фазовые портреты для бифуркации «двукратное равновесие» (случай а>0)

Будем следить за устойчивым положением равновесия. Тогда при приближении параметра к бифуркационному значению область притяжения этого равновесия с одной стороны уменьшается, и после исчезновения равновесий все решения уходят из рассматриваемой фазовой области. В приложениях такое явление называют «срывом равновесия».

Отметим, что при бифуркационных значениях параметров отображение проектирования многообразия на пространство параметров имеет особенность типа «складка» (рис. 3.3).

Пример: модель популяции, подвергаемой промыслу. Простым и выразительным примером бифуркации слияния пары равновесия (или бифуркации срыва равновесий) может служить модель превышения предельно допустимой интенсивности промысла популяции. Предположим, что в отсутствие промысла динамика численности популяции описы

Рис. 3.3. Слиянию двух положений равновесия отвечает особенность типа «складка»

вается логистическим уравнением, а в результате промысла из популяции изымается некоторое количество особей в единицу времени. Тогда динамика численности популяции описывается уравнением

где х-число особей, -скорость роста при малой численности, К-максимальная численность, определяемая доступными ресурсами, А- интенсивность промысла.

Нетрудно видеть, что — бифуркационное значение параметра, отвечающее слиянию равновесий.

На рис. 3.4 изображены события, происходящие при последовательном поэтапном усилении интенсивности промысла. Исходно не подвергаемая промыслу популяция находится в равновесном состоянии с численностью К- В мо

Рис 3 4 Динамика популяции, подверженной про­мыслу Превышение критической интенсивности промысла ведет к ее вымиранию

мент начинается промысел с интенсивностью , и численность популяции вслед за этим постепенно снижается до значения . В момент t₂ интенсивность промысла увеличивается до величины , и в популяции постепенно устанавливается численность - В момент t₃ интенсивность промысла принимает значение , большее критического (бифуркационного), и популяция вымирает.

Дата добавления: 2014-01-07