Бифуркация коразмерности два — трехкратное равновесие

Будем изменять значение параметров в системе (3.1), двигаясь по многообра­зию, определяемому бифуркационным ус-

ловием . Пусть при некоторых значениях параметров нарушается условие невырожденности для рассмотренной выше бифуркации коразмерности один, т. е. имеем одновременно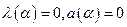

Тогда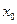— трехкратный корень уравнения (3.2).

Модельная система для данной бифуркации зависит от двух параметров и имеет вид:

, (3.7)

где .

Система (3.7) имеет две различные бифуркационные диаграммы, отвечающие различным знакам коэффициента 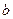. Пусть (случай приводится к данному заменой 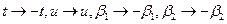). Бифуркационная диаграмма системы (3.7) при изображена на рис. 3.5. В системе (3.7) могут существовать одно или три грубых положения равновесия. Эти равновесия попарно сливаются на бифуркационных линиях , образующих полукубическую параболу с острием в точке 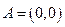. Этой точке отвечает слияние всех трех положений равновесия в одно. Для значений параметров, лежащих внутри полукубической параболы (область 2), в системе (3.7) имеются три

Рис 3 5. Бифуркационная диаграмма и фазовые портреты для бифуркации «трехкратное равновесие» (случай )

Рис 3 6 Слиянию трех положений равновесия отвечает особенность типа «сборка» Вблизи этой особенности система демонстрирует гистерезис

положения равновесия (два устойчивых и одно неустойчивое между ними), а для лежащих вне (область 1) — одно (устойчивое) положение равновесия.

Отметим, что при бифуркационных значениях параметров отображение проектирования многообразия 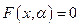на пространство параметров имеет особенность типа «сборка"» (рис. 3.6).

Динамическая система в окрестности данной бифуркации демонстрирует гистерезис. Будем менять параметры так чтобы пересечь полукубическую параболу (рис. 3.5), следя при этом за устойчивым равновесным режимом. Тогда при движении слева направо срыв равновесия произойдет на правой ветви полукубической параболы (S₂), а при обратном движении — на левой (). Это явление называют петлей гистерезиса.

Дата добавления: 2014-01-07