Распределение Ферми-Дирака

Найдем распределение ферми-частиц, т.е. частиц, обладающих полуцелым спином. Ферми-частицы подчиняются принципу (запрету) Паули, согласно которому в одном и том же состоянии одновременно не может находиться более одного фермиона. Т.е. можно сказать, что фермионы являются частицами-индивидуалистами. Рассмотрим идеальный ферми-газ, т.е. систему, состоящую из невзаимодействующих фермионов.

Сначала найдем число возможных распределений N частиц по Z ячейкам пенала при условии, что в каждой ячейке не может находится более одной частицы. Число ячеек Z и число частиц N должны удовлетворять условию Z ³ N.

Число всевозможных перестановок пустых ячеек пенала и ячеек с частицами равно Z!. При этом перестановки только ячеек с частицами в силу тождественности частиц не приводят к новым распределениям. Число таких перестановок равно N!. Перестановки местами пустых ячеек тоже не дают новых распределений, их число равно (Z - N)!. Таким образом, число различных распределений N частиц по Z ячейкам в данном случае равно:

.

Это выражение определяет число возможных распределений N фермионов по Z ячейкам, т.е. статистический вес макросостояния системы фермионов.

Вывод статистического распределения, которому подчиняются ферми-частицы, проводится также как и для бозе-частиц.

В шестимерном фазовом пространстве с координатами две изоэнергетические поверхност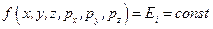и и 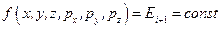выделяют тонкие энергетические слои. Опять предполагаем, что . Пусть в i -ом слое имеется Z _i ячеек и частиц. Тогда статистический вес подсистемы из частиц есть 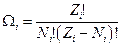. Статистический вес всей системы равен произведению статистических весов её отдельных подсистем:

.

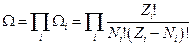Для того чтобы найти наиболее вероятное распределение частиц по ячейкам, нужно найти максимум статистического веса при условии, что полное число частиц системы N и полная энергия системы E остаются постоянными, т.е. 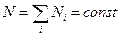и .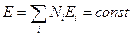

Как и для бозе-частиц, вместо максимума статистического веса W будем искать максимум энтропии :

.

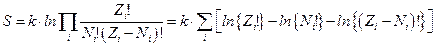Используем формулу Стирлинга: 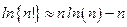, которая справедлива при . Поэтому при и , выполняется:

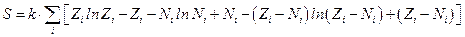или .

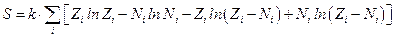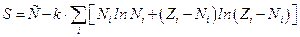, где .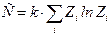

Слагаемое С можно в дальнейшем не учитывать, поскольку при решении задачи на экстремум энтропии S варьироваться будут только числа частиц в слое , а C от них не зависит.

Для отыскания максимума энтропии используем метод множителей Лагранжа. Рассмотрим функцию , где

,

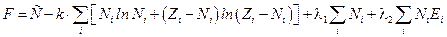а l₁ и l₂ - множители Лагранжа. Равенство нулю частных производных этой функции по :

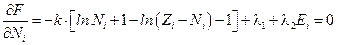, откуда .

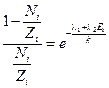Отношение 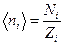представляет собой среднее число ферми-частиц, приходящихся на одну ячейку, т.е. на одно квантовое состояние: .

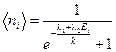Множители Лагранжа l₁ и l₂ находятся точно также как и в случае бозе-частиц: , , где m - химический потенциал. Тогда .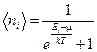

Освобождаясь от индекса i, приходим к окончательному выражению для среднего числа ферми-частиц, приходящихся на одно квантовое состояние:

.

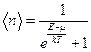Это соотношение называется распределением Ферми-Дирака. Оно определяет среднее число ферми-частиц, находящихся в квантовом состоянии с энергией E.

Следствия из распределения Ферми-Дирака.

1. не может быть больше единицы. Это означает, что в одном квантовом состоянии не может находиться более одной ферми-частицы, что согласуется с принципом Паули. Поскольку 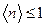, то говорят, что распределение Ферми-Дирака определяет вероятность заполнения энергетического уровня с энергией E при температуре T.

2. Химический потенциал m для ферми-частиц может быть только положительным, т.е. m>0. Иначе при T ®0 экспонента в знаменателе обратилась бы в бесконечность, а числа заполнения - в нуль, чего быть не может.

Рассмотрим случай малых чисел заполнения: 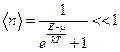. Это условие выполняется при 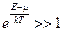, но тогда 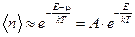, где 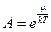, т.е. распределение Ферми-Дирака при малых числах заполнения (говорят, в случае разреженного ферми-газа) переходит в классическое распределение Больцмана. Т.к. в распределение Больцмана в случае малых чисел заполнения переходит также и распределение Бозе-Эйнштейна, то можно сделать вывод, что разреженные квантовые газы (и в случае бозонов, и в случае фермионов) не являются вырожденными и подчиняются классической статистике.

Принципиальное различие между распределениями Ферми-Дирака и Больцмана наблюдается при 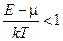. Классические частицы могут накапливаться в одном и том же состоянии в большом количестве. Для них тем больше, чем меньше энергия состояния E. Что же касается ферми-частиц, то максимальное их число в одном квантовом состоянии не может превышать единицу, что согласуется с принципом запрета Паули.

Химический потенциал m, который имеет размерность энергии, в случае ферми-частиц называют энергией Ферми или уровнем Ферми и обозначают E _F. При этом распределение Ферми-Дирака принимает вид:

.

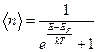Т.к. для фермионов m>0, то энергия Ферми E _F >0 также больше нуля. (Энергия Ферми E _F медленно меняется с изменением температуры T).

Рассмотрим зависимость распределения Ферми-Дирака от температуры. Будем считать, что рассматриваемая температура T может быть сколь угодно близка к абсолютному нулю, т.е. T ® 0. Обозначим через E_F (0) значение энергии Ферми при T ® 0. Этот случай будем условно называть случаем «нулевой температуры: T = 0». Из распределения Ферми-Дирака следует, что в случае T = 0:

.

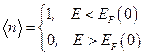Это означает, что все квантовые состояния с энергиями 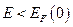оказываются занятыми фермионами, а все состояния с энергиями 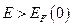- свободными. Таким образом, при T = 0 энергия Ферми E_F (0) является максимальной энергией, которой могут обладать ферми-частицы.

Распределение Ферми-Дирака в этом случае представляет собой ступенчатую функцию

единичной высоты, обрывающуюся при 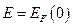. При отличных от нуля температурах резкий скачок < n > от единицы до нуля становится более размытым и происходит в области энергий, шириной порядка нескольких kT. Чем выше температура, тем шире область, в которой < n > меняется от единицы до нуля, и тем более плавно происходит переход от заполненных состояний к незаполненным. Однако, при любой температуре при E = E_F 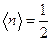. Т.е. в состоянии с энергией, равной энергии Ферми, всегда находится один электрон.

Наряду с энергией Ферми E_F при анализе поведения ферми-частиц вводятся также импульс Ферми p_F и скорость Ферми v_F, определяемые соотношениями: 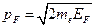, 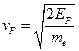. При T = 0 это максимальные импульс и скорость, которыми может обладать ферми-частица.

Дата добавления: 2014-01-07