
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 6. В общем случае можно рассматривать все перечисленные ранее переменные как компоненты многомерных векторных функций
|
|
|
|
В общем случае можно рассматривать все перечисленные ранее переменные как компоненты многомерных векторных функций. 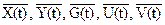 .
.
С точки зрения макроподхода аналоговые САУ с сосредоточенными параметрами можно описать системой дифференциальных равнений, связывающих входные переменные 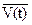 и выходные переменные
и выходные переменные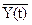 .
.
В общем случае эта система уравнений является нелинейной.
В простейшем случае для одномерной системы (один вход, один выход) система имеет вид:
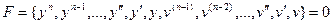 (1)
(1)
F- известная нелинейная функция. Уравнение (1) является уравнение динамики САУ. Для статического режима при постоянных входных переменных, когда
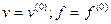 , процесс с течением времени устанавливается в пределах принятой (заданной) погрешности.
, процесс с течением времени устанавливается в пределах принятой (заданной) погрешности.
Выходная величина в этом случае равна константе 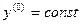
Уравнение (1) примет вид:
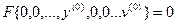 - уравнение статики САУ (2) (частный случай уравнения (1))
- уравнение статики САУ (2) (частный случай уравнения (1))
Для анализа процессов САУ и определения зависимости процессов от параметров системы необходимо каким- либо способом или методом получить решение уравнения 1 или 2.
При этом прежде всего необходимо наличие решений. Если решение есть, то каков их характер, т.е. устойчивость или неустойчивость.
В нелинейных системах высоких порядков возможно существование устойчивых периодических режимов из состояний равновесия. Отыскание таких режимов представляет собой задачу, не имеющую (к сожалению) аналитического решения.
Анализ существенно упрощается при использовании линейных или линеаризованных моделей.
Во многих случаях уравнение (1) можно линеаризовать. В нормально спроектированных САУ фактический режим отличается от требуемого в пределах заданных малых отклонений.
Малость этих отклонений позволяет произвести линеаризацию. В этом случае нелинейная функция (1) (нелинейные функции, входящие в уравнения) раскладывается в ряд, например в ряд Тейлора с точностью до линейного члена. САУ. Которые описываются линейными уравнениями называются линейными.
При линеаризации следует учитывать следующие факторы:
1.Отклонения 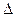 Y и
Y и 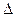 V соответственно по выходным и входным величинам должны быть достаточно малыми. Это условие зависит от вида нелинейности.
V соответственно по выходным и входным величинам должны быть достаточно малыми. Это условие зависит от вида нелинейности.
2.Функция F (1) должна обладать непрерывными частными производными по всем своим аргументам в окрестностях точек, соответствующих заданному режиму.(это условие разложения в ряд Тейлора).
Например для одномерно САУ уравнения (1) в линейном приближении можно преобразовать к виду:
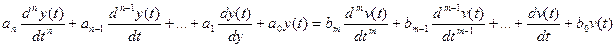 Правая часть- функция сигнала.
Правая часть- функция сигнала.
В уравнении 3 коэфициенты a0,a1,…,an, b1.,b2,…,bm- для стационарных САУ это константы. Это параметры системы. Стационарные САУ при постоянных внешних воздействиях описываются уравнениями, не зависящими в явном виде от времени t, т.е. свойства стационарных САУ во времени не меняются.
Стационарные линейные САУ описываются линейными уравнениями с постоянными коэффициентами.
Нестационарные линейные САУ описываются линейными уравнениями с переменными коэффициентами (САУ с переменными параметрами).
Согласно уравнению (3) в общем случае можно представить математическую модель линейной стационарной САУ в следующем виде:
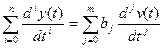 , где i=0,1,2… j=0,1,2…n (4)
, где i=0,1,2… j=0,1,2…n (4)
ННУ:
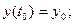
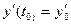
…
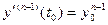
Условие (5): n>m (5)
Это условие физического существования системы.
В ТАУ принято стандартная форма записи дифференциальных уравнений. В качестве примера возьмем САУ 2-го порядка. n=2.
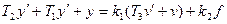 *
*

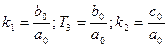
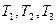 - постоянные времени [c]
- постоянные времени [c]
k-передаточные коэффициенты.
Для удобства исходное дифференциальное уравнение нормируют относительно производной низшего порядка переменной Y.
Уравнение * можно записать в символической форме:
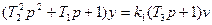
Уравнение 4 при независимых нач условий 4’ имеет единственное решение.
Аналитически это решение можно записать в форме суперпозиции 2-х решений (2-х реакций):
1.Реакция на начальные условия 4’ при V=0. Эта составляющая называется свободной составляющей и представляет собой сумму собственных колебаний, описываемых экспоненциальными функциями времени.
При 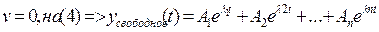 (6)
(6)
В математическом анализе эта составляющая называется общим решением.
A1,A2…An- произвольные постоянные интегрирования, которые зависят от начальных условий 4’
Вторая составляющая решения- реакция на ненулевое воздействие при V  0 при нулевых начальных условиях. Такая составляющая называется ПРИНУЖДЕННОЙ. (6’)
0 при нулевых начальных условиях. Такая составляющая называется ПРИНУЖДЕННОЙ. (6’)
Yпр(t)’ Можно представить суммой инвариантных функций. В матанализе- это частное решение, определяемое правой частью уравнения.
Инвариантные функции не изменяют свое формы при преобразованиях в системе. К ним относятся:
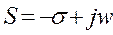
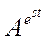
Показатель s называют комплексной частотой (6’’)
Также используются гармонические функции
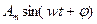 (6’’’)
(6’’’)
Гармонические функции можно рассматривать как экспоненциальные при 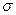 =0, т.е. при s=jw
=0, т.е. при s=jw
Например для САУ первого порядка n=1, а m=0
Решения уравнения 4 с начальными условиями 4’ имеет вид:
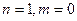
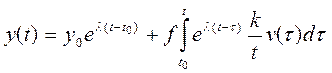 (7)
(7)
Общий вид решения- полный интеграл
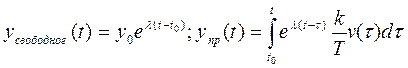 (8)
(8)
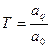 -постоянная времени системы.
-постоянная времени системы.
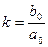 -Статический коэффициент системы
-Статический коэффициент системы
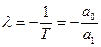 -корень характеристического уравнения системы.
-корень характеристического уравнения системы.
В теории управления заранее неизвестен вид воздействия V(t). Поэтому основная трудность заключается в определении реакции Yпринужденное(t) именно на произвольную функцию V(t).
Лекция 7
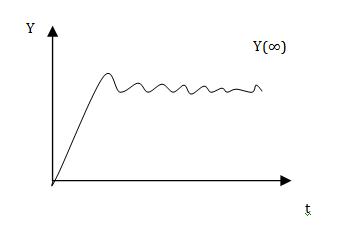
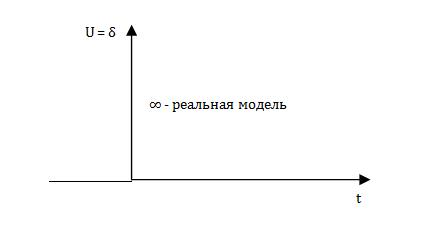
δ(t) – Функция Дирака
δ(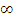 )
)
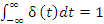
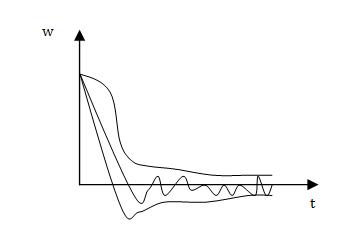

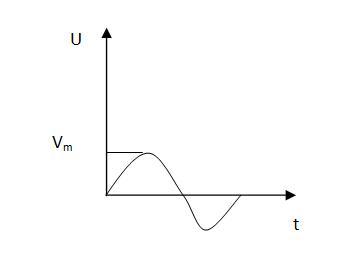
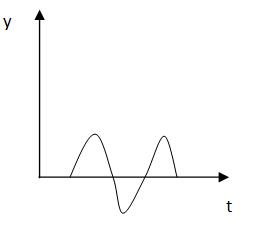
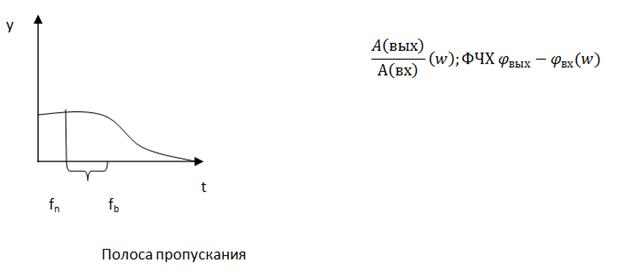
Для САУ при N=1:
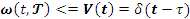
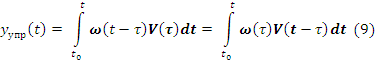
Желательно было бы получить некую формулу Yпр(t), которая включала бы в себя некоторую характеристику САУ, преобразующую входное воздействие V(t) в реакцию. Такой характеристикой может быть например
Характеристика - реакция системы на стандартное воздействие.
Физически функции Дирака не существует(Она выше)
Импульсная характеристика.
В частотной области это реакция системы на стандартное гармоническое воздействие.
Такой характеристикой может быть например: весовая характеристика w(t,τ) импульсная переходная функция. Ей соответствует воздейсвтие V(t) = дельта(t-τ) при нулевых начальных условиях.
В этом случае(Далее формулы в тетради)
Для САУ высоких порядков когда N>1.
для N>1
y(t)=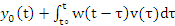 (10)
(10)
Где y0(t) свободная составляющая реакции в общем виде. Это есть линейная комбинация линейно независимых решений однородного линейного обыкновенного дифференциального уравнения, в котором произвольные константы определяются из независимых условий 4’. Если представлять воздействие V(t), совокупностью показательных(или гармонических функций) то произвольное воздействие V(t) можно выразить в этом случае через интегральное преобразование Фурье. Дело в том, что большинство физических реальных воздействий V(t) может быть представлено совокупностью экспанент или гармонических функций с использованием интегральных преобразовний Лапласа или Фурье. V(t) = интеграл от – бесконечности до бесконечности(Формула в тетради), где C(jw) = 1/2п…
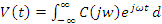 ω (11) где
ω (11) где
e(jw)= 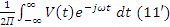
Выражения 11 и 11’ это есть обратное и прямое соответственно интегральное преобразование Фурье, а C(jw) это спектральная плоскость или спектральная функция сигнала V(t).
С учётом этого 11 и 11’ можем записать, что формула (12) 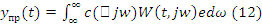
W(t,jw)
соответственно + ещё одна формула в тетради.(Формула АФЧХ нестационарной линейной сау омега от t и jw). Для стационарной линейной САУ t = 0 и W(t,jw) => W(jw) это АФЧХ. И таким образом мы имеем модуль W(jw) это АЧХ. Arg{W(jw)} = > ФЧХ. То есть это частотные характеристики для статических режимов работы САУ. Таким образом уравнение (10) это реакция или реализация модели в виде реакции имеет вид y(t)=y0(t) + интеграл от минус (Вообщем формула в тетради) (13)
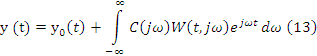
. Такой подход к представлению произвольного воздействия позволяет широко использовать частотные методы.(Передаточных характеристик при анализе и синтезе САУ, представленных линейными(Линеаризованными моделями).
Для многомерных объектов увеличивается число выходных величин, кроме этого возможно увеличение количество входных величин, поэтому многомерное САУ характеризуется уже системой дифференциальных уравнения типа вход-выход и уравнение 4 в этом случае будет иметь вид:
Формула в тетради сумма от а и джитое … (4’’)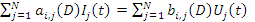 .
.
Где i = 1,2,3 … N; j = 1,2,3 … N.
Число управляющих переменных от j до N равно N и число Контроллируемых переменных равно тоже N.
Множители Aij(D) и bij(D) являются полиномами nij и mij степеней.
Условия физической реализуемости степени для этого случая принимает вид nij >= mij (4’’)
Оператор D – это оператор дифференцирования соответствующей степени. d/dt.
Систему 4’’ можно представить в матричной форме. Это будет матрица Формула [F*(D)]…(4’’’)
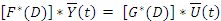
Матрица F*(D) и G*(D) состоят из элементов aij(D) и bij(D) эти матрицы могут быть представлены суммами матриц умноженных на оператор D в соответствующей степени.
[F*гамма(D)гамма+F формула. (4’’’’)
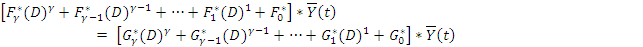
γ равно максимальному значению (nij)
Усложнение САУ и развитие численных методов анализа на базе матричной алгебры привели к использованию уравнения состояния при описании объектов и систем.
Это всё приводит к использованию микроподхода. В технических системах в качестве переменных состояния для физического описания САУ принимаются те переменные X больше с чертой от (t) для которых возможно определение независимых начальных условий. X большое с чертой от (tнулевое) на основе физических законов. Эти переменные должны полностью определять поведение системы при этом их должно быть минимально возможно количество. Уравнение состояния как правило представляют в форме КАШИ: в левой части только первые производные от переменных состояния в правой части линейные комбинации переменных состояния и воздействий. При этом правые части не содержат ни производных ни интегралов. Например при описании одномерного объекта система уравнений состояния будет иметь следующий вид: Рисунок в тетради.
Уравнение состояния. dx1(t) формула в тетради… (14).
 =
=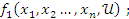 (14)
(14)
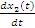 =
=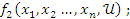
…
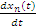 =
=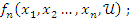
Систему 14 дополняют уравнениями выхода, связывающими переменную y(t) с переменными вектора x(t) и u(t).
Лекция 8
В результате получается система из уравнений динамики и уравнений выхода. В матричной форме такая система имеет вид:
d/dt …
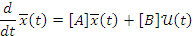
Уравнение динамики.
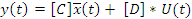 – Уравнение выхода
– Уравнение выхода
В системе 15 вектор x(t) вектор состояний. U(t) воздействие на объект.
Y(t) выходная переменная.
Матрица [A] матрица динамики.
Матрица [B] матрица входа.
[C] матрица выхода.
[D] матрица усилений по входу.
Замечание: для физически реализуемых систем и объектов в большинстве случаев матрица [D] равна 0.
Вектор X(t0) – вектор н.н усл.
Это и есть модель в пространстве состояний.
Устойчивость САУ её наблюдаемость и управляемость можно оценить исследовав коэффициенты матриц [A] [B] [C] и [D]. Матричные уравнения состояния можно получить преобразованием системы уравнений вход – выход. На практике уравнение состояния формируют на этапе составления модели объекта. Метод переменых состояния и анализ с использованием передаточных функции и частотных характеристик не исколючают, а взаимно дополняют при использовании численных процедур. И для того и для другого методов разработаны эффективные методы анализа систем большой размерности, а также типовые программные средства их реализации. Не надо боятся таких моделей.
Примеры составления уравнения состояния.
Пример №1.
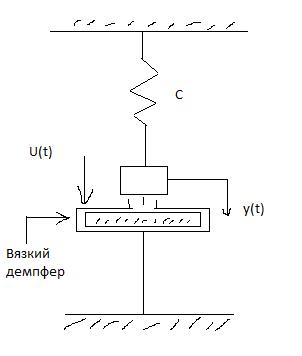
Рассмотрим простейшую механическую систему с упругим элементом(пружиной), массой и вязким демпфером. Структурная схема такой системы представлена на рисунке:
Рисунок
На массу действует воздействие U(t).
C – жёсткость пружины.
h – коэффициент демпфирования.
m – масса груза.
U(t) –возмущающая сила.
Y(t) – перемещение массы m.
Составим физическое описание системы.
На основе 2-го закона Ньютона имеем:
Формула(16,17)
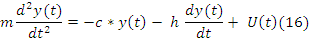
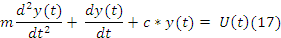
В момент t0 нам известны y(t0) и скорость dy(t)/dt при t0. Измеряются физическими приборами(Начальные условия).
На основании этого можем ввести вектор состояния.
На основании этого можем ввести вектор состояния X(t) = { x1(t),x2(t)}T согласно этому вектору уравнение 16 принимает вид: Формула(18)
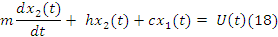
Дополним уравнение 18 следующим уравнением
Формула(18’)
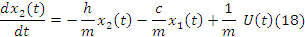
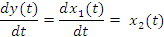
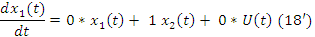
В результате мы получаем слудющую матричную форму:
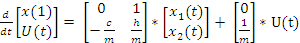 (19)
(19)
Матрицы в тетради.
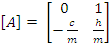 Матрица динамики
Матрица динамики
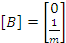 Матрица воздействия
Матрица воздействия
Дополняем уравнение динамики 19 и 20 уравнением выхода.
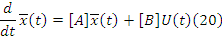
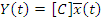
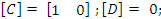
Y(t) это есть x1(t)
Формулы в тетради(21).
Пример 2.
Рассмотрим простейшую электрическую систему в виде последовательного колебательного контура из R,L,C.
Схема в тетради.
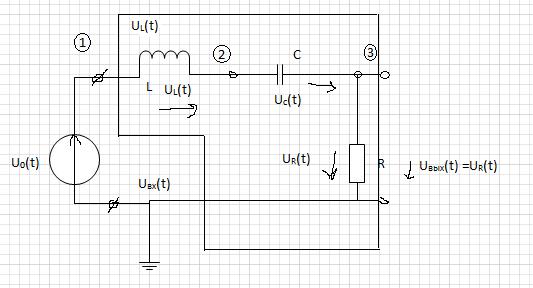
Дополним уравнение 26 уравнением выхода.
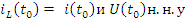
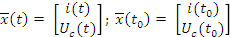
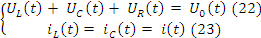
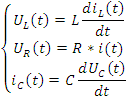
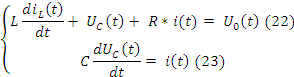
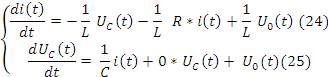
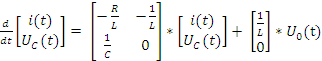
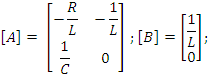
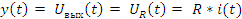

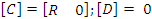
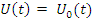
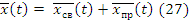
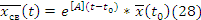
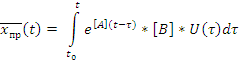
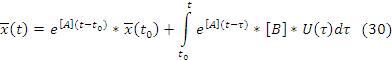
Выражение математической экспаненты:
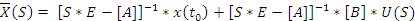
Уравнение динамики S области.
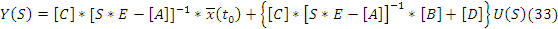
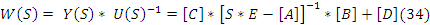
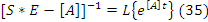
Решение непрерывного векторного уравнения состояния(Уравнения динамики) Можно реализовать на основе аналитического метода матричных экспанент). При этом полагаем что предварительно определены и известны матрица динамики А, матрица входа Б, воздействия U(t) при всех t>=t0. А также определён вектор начальных состояний(Независимые начальные условия). X(t0). В этом случае общий вид полного интеграла(Решения системы) будет иметь следующий:
27 в тетради
Где,
28.
Таким образом вектор x(t) есть
Пояснение.
В выражениях 28,29,30 матрица e в степени матрица [A]*t есть матричная экспонента или матрица перехода, которую можно представить в виде бесконечного ряда из матриц(выражение матричной экспаненты).
В области изображений по Лапласу. Решение 30 будет иметь вид:
В 33 мы избавились от интегралов и залезли в операции с матрицами.
E – единичная матрица.
Из уравнения 33 определяется передаточная функция.
34,35
Решение непрерывного уравнения состояния во временной области t (30) приводит к необходимости определения матричной экспаненты и интеграла свёртки матричной экспоненты с входным воздействием. Реализация решения 30 может осуществляться по разному например:
Если u(тау) представляет собой относительно не сложную функцию то интеграл свёртки, то интеграл свёртки можно определить аналитически. В этом случае саму матричную экспаненту целесообразно определять аналитически. Например по теореме Кели-Гамильтона смотри любой справочник по высшей математики, или по теореме Сильвестра. Решение в этом случае будет аналитческим. В виде аналитического выражения.
Если интеграл свёртки определяется весьма сложно, то его целесообразно определять приближёнными методами по любому подходящему алгоритму. В этом случае матричную экспаненту целесообразно опеделять численно по выражению (31), редуцируя этот ряд. Кроме этого возможна комбинация численного определения интеграла свёртки и аналитического определения матричной экспаненты или же использование разностных формул для решения (30).
Лекция 9
 (1)
(1)
 (2)
(2)
(3) U(B)
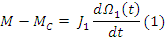
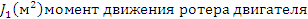
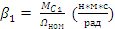 (5)
(5)
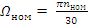 (6)
(6)
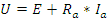 (7)
(7)
 (8)
(8)
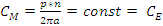 (9)
(9)
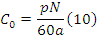
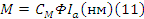
 (12)
(12)
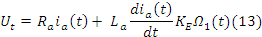
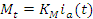 (14)
(14)
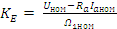 (15)
(15)
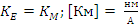 (15)
(15)
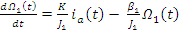 (16)
(16)
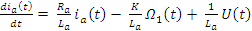 (17)
(17)
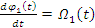 (18)
(18)
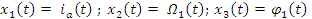 (19)
(19)
Решение в области s изображения по Лапласу избавляет в области s. В этом случае используются законы линейной алгебры. В результате получается аналитическое выражение изображения по Лапласу векторов X(s) и Y(s) эти изображения затем переводятся в область t. Например при помощи теоремы разложения или по таблицам. В результате перевода получаем X(t) и Y(t).
Замечание. Для многомерных объектов процесс определения уравнения состояния аналогичен процедурам, проведённым для одномерных объектов. Смотрите пример, однако в этом случае приходится оперировать соответствующими матрицами и векторами.
В теории автоматического управления с момента её возникновения широко использовались и развивались структурно-топологические методы описания и исследования систем. Структурная схема САУ строится на основе соединения типовых звеньев.
Типовые звенья отражают отдельные простые операции преобразования операции сигналов: усиление(пропорциональное изменение) Дифференцирование, интегрирование, и т.д.
Каждое типовое звено описывается дифференциальным уравнением, не выше 2-го порядка. Соединение элементарных звеньев отражает порядок прохождения сигналов в реальной САУ. Дифференциальные уравнения звеньев как правило записываются в области Лапласовых изображений “S” в форме передаточных функций и характеризуют преобразования сигналов при прохождении их через данное звено. Такой подход в описании САУ оказался весьма эффективным при анализе и синтезе аналоговых регуляторов и корректирующих устройств.
Топология в САУ (Способ соединения элементов существенно влияет на свойства элементов. При исследовании САУ, кроме математического аппарата передаточных функций шикроко используется теория графов и структурных методов.
Пример описания управления.
В качестве примера рассмотрим математическое описание исполнительного двигателя станочного электропривода. Для простоты будем рассматривать как базовый вариант исполнительный двигатель постоянного тока с неизменным возбуждением. (Неизменным магнитным потоком полюса индуктора) Так как математическая модель этого двигателя является относительно простой, её характеристики близки к линейным(Не все) и целесообразно её взять за базовую. Замечание:
Кроме ДПТ широко используется в современным станочных системах различные вентельные двигатели переменного тока, а также асинхронные двигатели, однако их математические модели такого же уровня описания на много сложнее математической модели упомянутого ДПТ.
ДПТ с неизменным возбуждением(Неизменным магнитным потоком полюса индуктора).
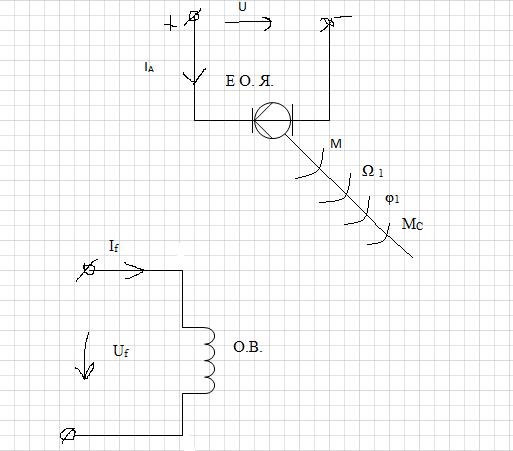
Исходная информация об объекте. ДПТ с независимым возбуждением это может быть по схеме включения как с независимым возбуждением так с параллельным или последовательным возбуждением. Это по схеме включения. В качестве примера рассмотрим ДПТ с независимым возбуждением. В этом случае обмотка якоря имеет свой источник, а обмотка возбуждения(индуктора) имеет свой источник независимый от источника якоря. Кроме того вместо обмотки возбуждения могут быть постоянные магниты. Оба этих варианта предполагают, якорный способ управления двигателем, т.е. управлением осуществляется по цепи обмотки якоря, например за счёт изменения напряжения U на обмотке якоря в этом случае поток полюса фи(t) индуктора остаётся практически неизменным. (Это допущение о пренебрежении реакции искажения результирующего поля за счёт реакции якоря.) Фи(t) равен const.
Схема включения (1).
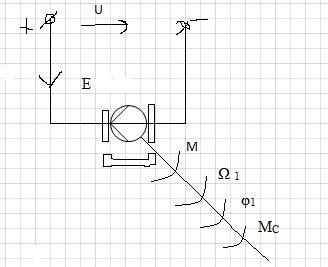
Схема включения (2).
Выписываем (3).
U(в) – источник постоянного напряжения на обмотке якоря.
Uf(в) – постоянное напряжение на обмотке возбуждение.
Реакции на решающие возбуждения:
Ia(A);If(A)
E(в) – ЭДС в обмотке якоря.
На валу:
M(Нм) – электромагнитный момент развиваемый двигателем.
Mс(Нм) – вопрос сопротивления на валу двигателя.
Ω1 (Рад/сек) – угловая частота вращения вала двигателя.
φ1 (Рад) – угловое перемещение вала двигателя.
Для составления уравнений состояния ДПТ воспользуемся известной нам информацией основанной на физических законах.
Уравнение движения(Ссылаясь на картинку).
(4) Уравнение равновесия моментов.
Момент сопротивления. В самом простом варианте моментом сопротивления является момент вязкого трения ротора.
Пусть Мс = Мс1 = бетта1 * Ω1(Н*м)
Где (5) приведённые коэфицент трения.
(6). Номинальная частота вращения.
Где nном(об/мин) – паспортные данные.
Уравнение статического равновесия цепи якоря.(Закон киргофа)
(7). В статическом режиме, где E – определяется по (8)
Ra активное сопротивление обмотки якоря, либо паспортные данные либо измеряется физические приборы.
CE конструктивная константа двигателя. (9).
p – число пар полюса, паспортные данные.
N число
Число параллельных ветвей обмотки якоря паспортные данные.
Фи(Вб) – магнитные поток полюса индуктора.
(10)
Электромагнитные момент развиваемый якорем двигателя (Ротером) (11).
Учитывая предидущие допущения о неизменности потока φ можем константы E и M принять за константы и обозначить как (12).
В динамике уравнения (7) принимает вид (13)
Уравнение (12) принимает вид (14).
La индуктивность обмотки якоря в (Гн) паспортные данные.
KE.
Рассчёт КМ и КЕ. (Коэфициент момента и скоростной коэфицент)
(15)
Перепишим уравнение движения с учётом уравнения (14) и Mc в (16).
Перепишем (13) в (17)
Математическое описание ДПТ в пространстве состояний.
Во многих слуачаях не все переменные управляемых объектов измеримы и доступны измерению. Измеримыми являются лишь те, которые составляют выходной вектор Y(t). Среди измеримых переменных обычно находятся и управляемые переменные. Число взаимно независимых управляемых переменных определяет размерность системы уравнения состояния.
Порядок системы уравнений равен число переменных состояния, для нашего объекта можем добавить к уравнениями 9 и 10 выражение (18).
В соответствии с уравнениями 16,17,18 введём вектор переменных состояния. (19).
Лекция 10
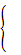
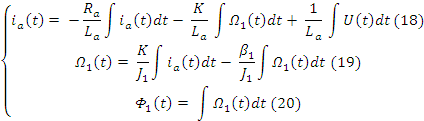
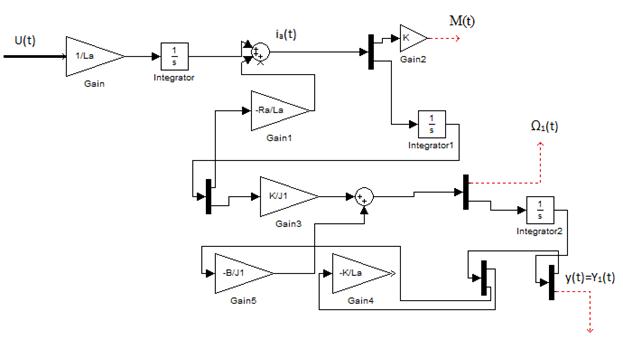
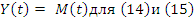
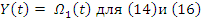
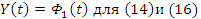
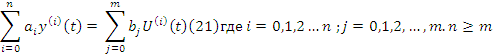
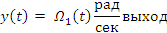
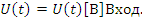
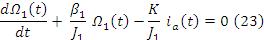
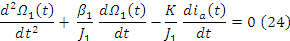
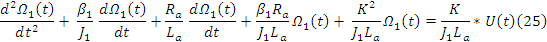
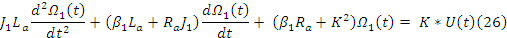
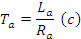
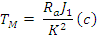
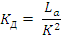
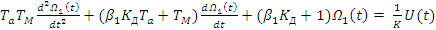 (27)
(27)
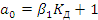
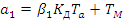
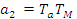
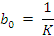
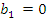

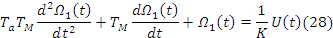
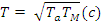
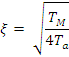
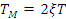
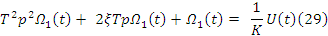

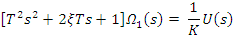
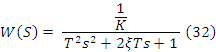
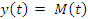
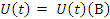
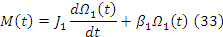
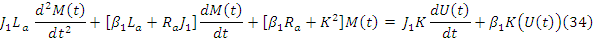
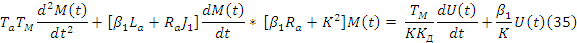
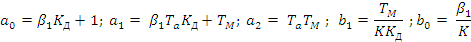
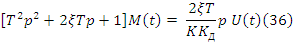
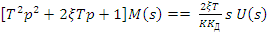 (37)
(37)
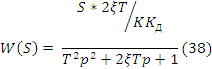
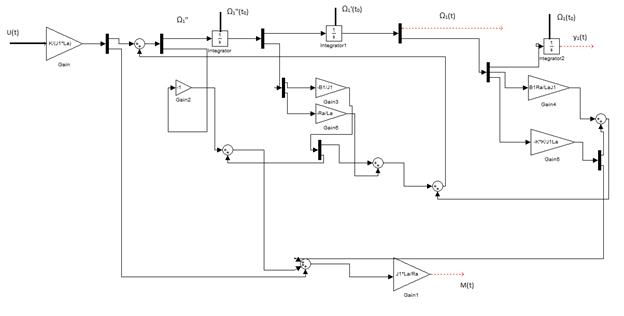
При составлении структурной схемы модели следует исключить ввиду рядов причин использование дифференцирующих блоков. Предпочтительно построение схемы на базе пропорциональных блоков интеграторов, сумматоров. Перепишем уравнение 9,10,11, проинтегрировав их левые и правые части. Получаем (1).
Система18-20 не содержит производных.
Принцип построения схемы следующий:
(рис. 2)
Блок схема в модели ДПТ в программе состояний.
При составлении уравнения в координатах вход – выход также как и при описании объектов в пространстве состояний в качестве основы необходимо использовать информацию об объекте. Эта информация основана на физических законах. Как правило такая информация описывает колличественно описывает какую либо из сторон реальных процессов в объекте. В нашем случае для ДПТ можно использовать в качестве начальной информации уравнения от 1 до 10. Однако необходимо выбрать из этих уравнений те, которые уже содержат в удобной форме принятые нами переменные входа и переменные выхода. Наиболее удобными в данном случае являются уравнения 9 и 10. В качестве желаемой, окончательной форме представления модели примим следующую форму: (3).
Пусть (4).
В уравнении 9 присутствует омега.
Перепишим уравнение 9 в следующем виде: (5).
Продифференцировав 23 получаем. (6).
Подставим в 24 из уравнения 10 выражение производной dia(t) / dt. (7).
26 – это окончательный результат.
Перепишем 26 введя общепринятые в ТАУ и теории электрических машин постоянные, которые зависят только от параметров двигателя.
Ta электромагнитная постоянная времени (8) секунды.
TM электромеханическая постоянная времени двигателя. (9).
Kд – постоянная двигателя.(10)
Все эти постоянные можно определить по соответствующим паспортным данным двигателя или по данным каталога.
В результате относительно несложных преобразований и подстановок уравнение 26 примет вид.(11)
Уравнение 28 можно переписать введя ещё одни обозначения.(12)
В этом случае в операторной форме она будет иметь ввид: (13)
В уравнениях 29, 30 зетта коэффициент дельпфирования.
В области изображения по лаплассу перепишем: (14)
Соответственной имеем звено 2-го порядка которое может быть в зависимости от значения коэфициента зетта либо колебательным либо апериодическим.
Коэффициент зетта в свою очередь определяется параметрами двигателя Тм и Та
Эта модель имеет соответствующие частотные и временные характеристики. АЧХ, ФЧХ, переходную и импульсную. Если в качестве выходной переменой рассматривать электромагнитный момент, а в качестве входной U(t).
Т.е. если (15)
Для получения модели объекта в форме 29 можно получить уравнения 9 переписав его соответствующим образом с учётом выражений 6 и 8.
Получается (16).
После несложных преобразований и подстановок с учётом уравнения 8 получаем из 33 (16)
Уравнение 34 с учётом принятых ранее обозначения будет иметь вид: (17)
Вывод коэффициенты a0 a1 a2 - совпадают с коэффициентами из уравнения 27,а отличаются только b1 b0 Учитывая принятые ранее константы T и дзетта для случая бетта 1 равное 0 (принебрежения вязким трением получаем уравнения упрощённой (18)
В области изображения по лапласу (19)
Структурная схема модели ДПТ в координатах вход-выход во временной области. Базовым является уравнение (27) и (35).
Принцип построения один и тот же, что был рассмотрен нами ранее для системы уравнения состояния.
Рисунок(20)
Независимые начальны условия.
Структурные схемы модели ДПТ в координатах вход выход в области изображений по Лапласу.
Лекция 18 апреля. // Это копия 10-й
При составлении структурной схемы модели необходимо стремиться исключить в силу целого ряда причин использование диффиренцирующих блоков. Предпочтительно построение схемы на базе пропорциональных блоков, интеграторов и сумматоров. Поэтому перепишем уравнение 9-10-11, проинтегрировав их левые и правые части. РИС 1
При составлении уравнения в координатах вход-выход также как и при описании объектов в пространстве состояний в качестве основы необходимо использовать информацию об объекте. Эта информация основана на физических законах. Как правило такая информация описывает количественно какую-либо из сторон реальных процессов в объекте. В нашем случае для LGN можно использывать в качестве начальной информации уравнения от 1- до 10. Однако необходимо выбрать их этих уравнений те, которые уже содержат в удобной форме принятые нами переменные входы и переменные выхода.
Наиболее удобными в данном слчае являются уравнения 9, 10. В качестве желаемой (окончательно) формыпредставления модели объекта примем:
Рис 2
Лекция 25 апреля (предпоследняя)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!