Коэффициент перекрытия косозубой передачи

Коэффициентом перекрытия ε_у называется отношение угла перекрытия φ_у к угловому шагу τ.

τ = 2 π / z.

Полный угол φ_у перекрытия в такой передаче состоит из двух слагаемых: угла торцового перекрытия φ_α и угла осевого перекрытия φ_β:

φ_у = φ_α + φ_β.

Углом φ_α торцового перекрытия (как и в прямозубом зацеплении) называется угол, на который поворачивается колесо от момента входа в зацепление торцового профиля зуба до выхода из зацепления этого профиля.

Углом φ_β осевого перекрытия называется угол, на который поворачивается колесо от момента выхода из зацепления торцового профиля зуба до выхода из зацепления зуба в целом.

Коэффициентом перекрытия ε_у = (φ_α + φ_β)/ τ = ε_α + ε_β ,

где ε_α и ε_β коэффициенты торцового и осевого перекрытия соответственно.

Коэффициент торцового перекрытия ε_α определяется также как для прямозубого зацепления.

На рис. 5.20 показана развертка делительной окружности косозубого колеса на плоскость.

Линиями 1 и 3 обозначены положения зуба в начале и конце зацепления. Линией 2 – положения зуба в момент выхода из зацепления в нижнем торцовом сечении.

Из рис.5.20 следует, что: ; ,

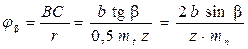где b – ширина колеса.

Рис. 5.20. К определению коэффициента перекрытия

Коэффициентом осевого перекрытия ε _β = φ _β /τ откуда:

.

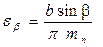Коэффициент торцового перекрытия ε_α определяется также как для прямозубого зацепления.

Итак: ,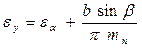

где ε _α – коэффициент торцового перекрытия, который определяется также как для прямозубого зацепления.

Итак, коэффициент перекрытия косозубой передачи увеличивается с ростом угла наклона зуба β и ширины колес.

Дата добавления: 2014-01-07