Статистическое определение вероятности

ЧАСТЬ 2. Вероятность

Пусть проведена серия из n испытаний при одних и тех же условиях; при этом фиксируется появление события А.

Допустим, что событие А произошло m раз. Число m называют частотой наступления события А. Ясно, что .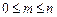

Относительной частотой события называют отношение 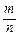− числа испытаний, в которых событие появилось, к числу всех проведенных испытаний.

Обозначение относительной частоты: 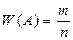. (6.1)

Если проводить серии опытов с большим числом испытаний при одинаковых условиях, то во многих случаях относительная частота наблюдаемого события будет мало меняться от серии к серии. Этот факт проверен многократно в различных экспериментах.

Определение.(статистической вероятности). Число, около которого группируются относительные частоты при увеличении числа испытаний, называют вероятностью рассматриваемого события А и обозначают P(A).

Основной недостаток статистического определения вероятности состоит в необходимости проведения большого числа опытов. Стоит заметить, что именно благодаря большому количеству опытов мы получаем наиболее близкое к реальному значение вероятности. Это экспериментальное определение значения вероятности и поэтому оно соответствует вероятности реального события с максимальной точностью, позволяет прогнозировать вероятность события для конкретного опыта.

Пример. В некотором районе зарегистрировано рождение с начала года 1248 младенцев, из них 645 мальчиков. Какова вероятность рождения мальчика в данном районе?

Решение: За вероятность принимаем относительную частоту рождения мальчиков. W = 645/1248 ≈ 0,517

Пример. Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, студенты провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:

Таблица 6.1

Цвет волос жителей города

Цвет волос	Брюнеты	Шатены	Рыжие	Блондины	Всего
Число людей

Оцените вероятность того, что выбранный наугад житель этого города будет: а) шатеном; б) рыжим; в) не блондином.

a) m = 372, n = 865, P(A) = m/n=372/865» 0,430;

б) m = 83, n = 865, P(A) = 83/865» 0,096;

в) m = 865-212 = 653, n = 865, P(A) = 653/865» 0,755

Пример. По статистике в городе N за год из каждой 1000 автомобилистов семь попадают в аварию. Какова вероятность того, что автомобилист в этом городе весь год проездит без аварий?

Решение. m = 7, n = 1000, P(A) = 7/1000 = 0,007 (вероятность попасть в аварию в течение года), отсюда вероятность проездить без аварий 1 – 0,007 = 0,993.

Классическое определение вероятности

Наступление каждого события зависит от многих факторов, заранее учесть которые обычно невозможно. Однако в случае совокупности однородных (массовых) событий можно обнаружить закономерности, позволяющие предсказать, насколько достоверно наступление того или иного события, т.е. насколько это событие вероятно.

Понятие вероятности вводится для того, чтобы выражать на языке чисел степень возможности наступления тех или иных событий.

За единицу принимают вероятность достоверного события, а вероятность невозможного события считают равной нулю. Тогда вероятность Р любого события А удовлетворяет неравенству:

0≤Р(А)≤1. (6.2)

Определение. События называются равновозможными, если ни одно из них не является более возможным, чем другое.

Примеры. Опыт состоит в подбрасывании монеты, событие А – выпадение орла, событие В – выпадение решки. Эти события равновозможные. Примером не равновозможного события может служить результат двукратного подбрасывания монеты: (1) выпадение двух орлов, (2) выпадение двух решек, (3) выпадение одного орла и одной решки. Равновозможными будут упорядоченные результаты двух подбрасываний монеты: (1) орел, орел; (2) орел, решка; (3) решка, орел; (4) решка, решка.

Определение. События А, В, С, …, К называются единственно возможными, если в результате опыта (испытания) одно из них обязательно наступит. То есть появление одного из них в результате опыта является достоверным событием. Говорят, что единственно возможные события образуют полную группу событий.

Пример. Подбрасывание монеты: события А (выпадение орла) и В (выпадение решки) образуют полную группу событий и являются единственно возможными.

Рассмотрим классический метод определения вероятности некоторого случайного события. Пусть в результате некоторого опыта могут наступить события А₁, А₂, А₃, …, А_n (элементарные исходы опыта), которые являются: 1) единственно возможными, т.е. в результате опыта хотя бы одно из них обязательно наступит; 2) несовместными, т.е. появление одного из них исключает появление всех остальных; 3)равновозможными, т.е. не существует никаких причин, в связи с которыми одно из событий появлялось бы чаще, чем остальные.

Пусть при появлении некоторых из этих событий наступает событие А. Обозначим число таких событий k (k≤n). А при появлении остальных (n-k) событий событие А не наступает. Говорят, что k событий (элементарных исходов), при которых появляется событие А, благоприятствуют событию А, а остальные (n-k) событий не благоприятствуют ему.

Определение. (Классическое определение вероятности). Вероятностью события А называется отношение числа k элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n, если они равновозможны, несовместны и единственно возможны. Обозначают:

Р(А)=k/n (6.3)

(от латинского слова probabilitas – вероятность).

При использовании данной формулы нахождение вероятности сводится к нахождению числа всех возможных событий в данном опыте и числа событий благоприятствующих событию А. Получаем теоретическое предположение о вероятности события.

Пример. Набирая номер телефона, вы забыли последнюю цифру и набрали ее наугад. Какова вероятность того, что набрана нужная цифра?

Решение: Ясно, что число всех элементарных исходов n=10. Все они равновозможны, несовместны и единственно возможны. Поэтому можно применить классическое определение вероятности. Число благоприятствующих исходов k=1. Поэтому Р(А)=1/10.

Пример. Из слова “математика” выбирается наугад одна буква. Какова вероятность того, что это будет буква «м»?

Решение: Пусть событие А – состоит в случайном выборе из данного

слова буквы «м», тогда, т.к. n=10 и k=2, то Р(А)=2/10=1/5.

Пример. В ящике 5 черных, 7 красных, 8 белых шаров одного материала, размера, степени и способа обработки, температуры. Наудачу взят один шар. Найти вероятность того, что он красный.

Решение. Любой красный шар из семи есть благоприятствующий исход событию А – взят красный шар. Всего же исходов 5+7+8=20. Применимо классическое определение: .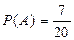

Пример. Из 13 книг, среди которых 8 справочников, отобрано 9 книг. Найти вероятность того, что среди отобранных книг – 5 справочников (событие А).

Решение. Будем считать исходами любые группы из 13 книг по 9. Таких групп конечное число и вероятность отбора любой из них одинакова. Применимо классическое определение вероятности.

Отбираемые группы отличаются хотя бы одной книгой (элементом), причем порядок книг в группах безразличен. Число таких групп равно числу сочетаний из 13 элементов по 9, т.е.

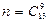, где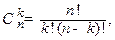

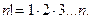
Благоприятные исходы – это те группы, в которых по 5 справочников. Чтобы найти их число, выделим среди книг справочники: 13=8+5. Число различных групп, составленных из 8 справочников по 5, равно 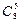, а из оставшихся 5 книг по 4 книги − 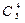. Объединяя (комбинируя) эти группы различными способами, получим благоприятные исходы. Их число .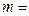

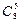
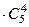По классическому определению,

.

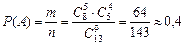Практический смысл полученного результата: если из 13 книг отбирать многократно по 9, то в среднем 4 раза из 10 (в 40% случаях) отобранная группа книг будет содержать 5 справочников.

Пример. В студенческой группе 20 человек, среди которых 5 отличников. Деканат случайным образом отобрал от группы для участия в конференции трудового коллектива 3 человек. Какова вероятность, что среди них окажется 2 отличника, которые сорвут план двоечников голосовать за удаление из учебной программы факультета дисциплины «Математика»?

Решение: N = 20 (общее количество студентов в группе), m = 5 (количество отличников), n = 3 (количество отобранных на конференцию), k = 2 (количество отличников среди отобранных).

Тогда искомая вероятность:

Пример. В библиотеке имеется 5 методичек выпуска 2009 года и 9 методичек по той же теме выпуска 2011 года. Библиотекарь выдает на группу 6 методичек. Какова вероятность того, что первой пришедшей группе будет выдано 5 методичек выпуска 2011 года, если библиотекарь берет методички произвольно?

Решение: Пусть A – искомое событие. Согласно классической формуле вероятность искомого события равна:

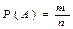, где m – количество благоприятных исходов; n – количество благоприятных исходов.

Имеем неупорядоченную выборку (порядок выбора методичек не имеет значения) без повторений (одну и ту же методичку нельзя взять два раза). Следовательно, имеем:

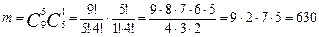
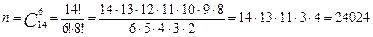
Отсюда вероятность того, что первой пришедшей группе будет выдано 5 методичек выпуска 2011 года равна:

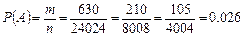
Дата добавления: 2014-01-07