Геометрическое определение вероятности

Свойства вероятностей

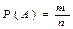1) , т.к. , а .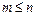

2) 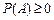, т.к. .

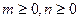3) 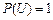, т.к. .

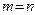4) , т.к. .

Если число равновозможных исходов бесконечно, и они целиком заполняют некоторую область, то используют геометрическое определение вероятности.

Рис. 6.1. К геометрическому определению вероятности

Пусть каждый результат испытаний определяется случайным положением точки в некоторой области, мера которой G (рис.6.1). Под мерой области будем понимать длину, площадь, объем. Если 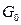− мера той области, попадание в которую благоприятствует событию А, то .

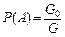Геометрическое определение: вероятность события А есть отношение мер областей 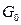(попадание в которую благоприятствует событию А) и (попадание в которую равновероятно, равно возможно и единственно возможно при данном опыте или испытании).

Пример. На отрезке 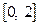наудачу выбраны два числа x и y. Найти вероятность того, что эти числа удовлетворяют неравенствам:

Решение. Нам известно, что и 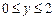. Для их изображения воспользуемся системой координат. Точки с координатами 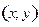заполнят квадрат со стороной, равной ед. Решим графически систему неравенств: , .

Рис. 6.2. Графическое решение системы неравенств

Применим геометрическое определение вероятности, причем в качестве меры областей выступает площадь.

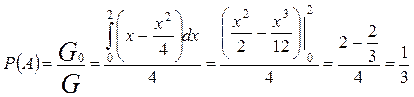
Пример. Точку наудачу бросили на отрезок [0; 2]. Какова вероятность ее попадания в отрезок [0,5; 1,4]?

Решение. Здесь пространство элементарных исходов весь отрезок G = [0; 2], а множество благоприятствующих исходов G0 = [0,5; 1,4], при этом длины этих отрезков равны G=2 и G0=0,9 соответственно. Поэтому P(A)=G0/G=0,9/2=0,45

Пример. Два студента условились встретиться в около столовой между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего идет обедать один. Чему равна вероятность встречи двух студентов, если приход каждого из них может произойти наудачу в течении указанного часа и моменты прихода независимы?

Решение. Обозначим момент прихода студента 1 через х и студента 2 – через у. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы ôх-уô£20. Изобразим х и у как координаты на плоскости, в качестве единицы масштаба выберем минуту. Всевозможные исходы представляются точками квадрата со стороной 60, а благоприятствующие встрече располагаются в заштрихованной области. Искомая вероятность равна отношению площади заштрихованной фигуры (рис.6.3) к площади всего квадрата: P(A) = (602–402)/602 = 5/9.

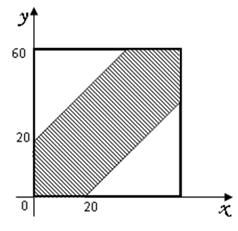
Рис. 6.3. Графическое решение примера

Дата добавления: 2014-01-07