Определение 2

Сходящиеся последовательности. Основные определения

Определение 1. Последовательность {x_n} называется сходящейся ({x_n}Îс), если существует такое действительное число а, что последовательность {x_n - а} является бесконечно малой последовательностью

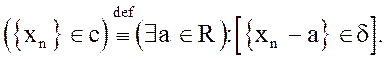
Замечание. Исходя из этого определения следует, что всякая бесконечно малая последовательность является сходящейся и имеет своим пределом 0.

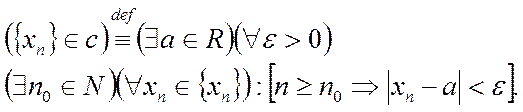
Очевидно, что неравенство | x_n - а|<e эквивалентно неравенствам

-e< x_n -а < e или а-e< x_n< а+e, которое означает, что некоторый элемент x_n последовательности { x_n } принадлежит e, окрестности числа а, поэтому определение сходящейся последовательности можно дать следующим образом:

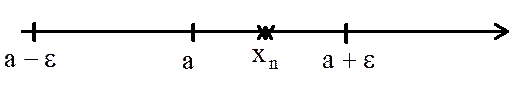
Определение 3. Последовательность {x_n} называется сходящейся, если существует действительное число а такое, что в любой e - окрестности числа а находятся все элементы последовательности {x_n} начиная с некоторого номера. Число а, фигурирующее в определениях, называется пределом последовательности {x_n}.

Символическая запись существования предела последовательности {x_n}, равного а, записывается так: , или {x_n}®а при n®¥.

Бесконечно большие последовательности иногда называются последовательностями, сходящимися к бесконечности, поэтому если {x_n}ÎБ, то символически это записывается следующим образом:

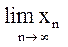= ¥, или {x_n}® ¥ при

n® ¥.

Если элементы бесконечно большой последовательности начиная с некоторого номера имеют определенный знак, то говорят, что {x_n} сходится к бесконечности определенного знака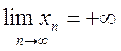

или .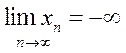

Замечание 1. Из определения 1 сходящейся последовательности вытекает, что последовательность {x_n - а}Îd. Обозначая элементы этой последовательности через a_n, a_n= x_n -а, мы получим, что любой элемент x_n сходящейся последовательности {x_n}, имеющей пределом число а, может быть представлен в виде x_n =a+a_n, где a_{n -} элемент бесконечно малой последовательности.

Замечание2. Из определения предела последовательности вытекает, что конечное число элементов не влияет на сходимость этой последовательности и на величину ее предела.

Пример. Покажем, что последовательность

{1+ (-1)ⁿ/n}сходится. Пределом этой последовательности является число 1. Для доказательства достаточно показать, что последовательность

{x_n - а}= {(-1)ⁿ/n}Îd. В самом деле, если n ³ n₀ , то поэтому по данному e>0 следует выбрать номер n₀ такой, чтобы выполнялось условие 1/n₀ <e, т.е.

n₀ =[1/e]+1, где [x]- целая часть числа x - т.е. наибольшее целое число, не превышающее x.

(Например, [6,187]=6; [-5,87]=-6).

В качестве n₀ можно взять и любой номер [1/e]+к, где к>1.

Дата добавления: 2014-01-07