Бесконечно малые и бесконечно большие функции

Пусть y=a(x) определена на {x} и а - предельная точка для {x}.

Определение 1. Функция a(x) называется бесконечно малой в точке а (при x®а), если (обозначение: a(x)=o(1)).

Определение 2. (по Гейне). Функция a(x) называется бесконечно малой функцией в точке а, если

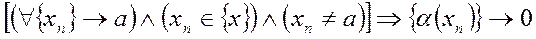
Определение 3. (по Коши).

.

Замечание 1. Через d(x₀) будем обозначать класс бесконечно малых в точке x₀ функций.

Теорема 1. Для того, чтобы функция y=f(x) имела равный b предел в точке a, необходимо и достаточно, чтобы функция a(x)=f(x)-b являлась бесконечно малой в точке a.

Необходимость. Пусть , тогда рассмотрим функцию a(x)=f(x)-b. Так как 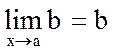, то , т.е. a(x)Îd(a).

Достаточность. Пусть , тогда f(x)= a(x)+b и , т.е. .

Определение 4. Функция y=f(x) называется бесконечно большой в точке a (f(x)ÎB(a)), если .

Обозначение: .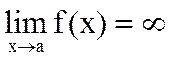

Аналогично даются определения .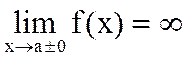

Пример. 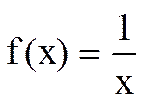является бесконечно большой в т. a=0.

Действительно, следующая импликация определения очевидна:

.

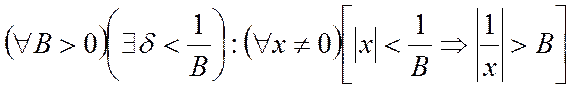Кроме того, .

Определение 5.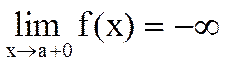

.

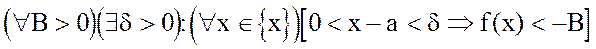Определение 6.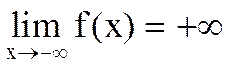

.

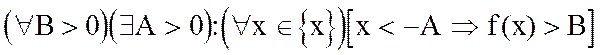Аналогично даются определения: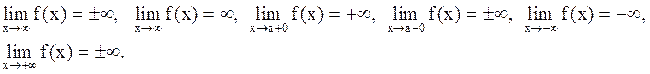

Пусть a(x) и b(x) - бесконечно малые в т. a функции, тогда

1) a(x) называется бесконечно малой более высокого порядка, чем b(x), если 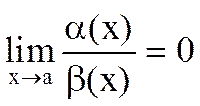(Обозначения: a(x)=o(b(x))). Читается: a есть o малое от b.

2) a(x) иb(x) называются бесконечно малыми одного порядка в т. a, если (Обозначения a(x)=0(b(x))). Читается: a есть 0 большое от b.

3) a(x) иb(x) называются эквивалентными бесконечно малыми в т. а, если (Обозначения: a(x)~(b(x)).

4) Бесконечно малая в т. а функция a(x) имеет порядок малости m относительно некоторой бесконечно малой в т. а функции b(x), если .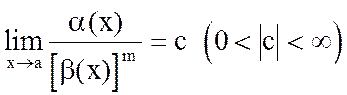

Замечание 2. Если не существует 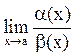, то a(x) иb(x) называют несравнимыми бесконечно малыми функциями.

Из определения 5 вытекают следующие утверждения:

1) o(b)±o(b)=o(b);

2) g=o(b)Þ o(b)±o(g)=o(b);

3) a=o(1), b=o(1)Þ ab=o(a),ab=o(b).

Докажем, например, утверждение 2). В силу утверждения 1) для этого достаточно доказать, что .

Пусть r=o(g). Это значит, что Нужно доказать, что 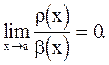Доказательством является целая цепочка равенств

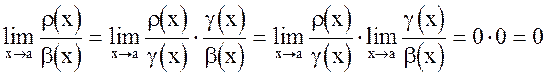
Докажем еще одно утверждение:

4) a~b Ûb=a+o(a)Úb=a+o(b)

Доказательство: а) a~b Þb=a+o(a) (см. теорему этого пункта)

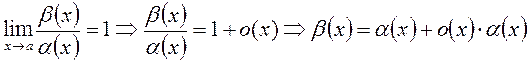
В силу утверждения 3) o(x)×a(x)= o(a), поэтому

б)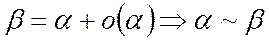

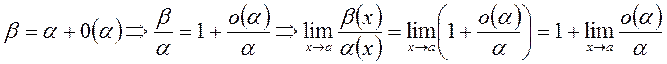
Но 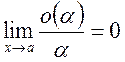в силу определения o(a), поэтому .

Аналогично доказывается, что a~b Û b=a+ o(b).

Таким образом, если b(x)~a(x), то a(x) приближает функцию b(x) при x®а (и наоборот).

Замечание. Свойство 1) o(b)-o(b)=o(b) означает следующее:

a₁=o(b), a₂=o(b)Þ a₁ - a₂=o(b). [a₁ - a₂ ¹0, вообще говоря, т.к. это разные функции, обозначенные одним символом o(b)].

Аналогично бесконечно малым сравниваются бесконечно большие в данной точке функции.

Пусть 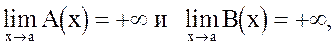тогда

1) А(x) имеет в т. а более высокий порядок роста, чем В(x), если

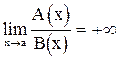
2) А(x) и В(x) имеют в т. а одинаковый порядок роста, если

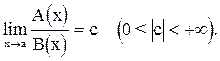
3) Бесконечно большая функция А(x) в точке а называется величиной к-го порядка относительно бесконечно большой функции В(x), если

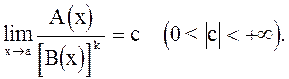
4) А(x) и В(x) называются эквивалентными в точке а, если

.

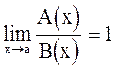5) Если не то А(x) и В(x) называются несравнимыми.

Замечание 2. Эти определения сохраняются для бесконечно больших функций в точке а слева и справа.

Пример. 1) a(x)=x³ - x⁵, b(x)=5x³ +x⁴, x®0. Эти функции бесконечно малые в т. x=0 одного порядка; действительно,

2) - бесконечно большие одинакового порядка роста при x®0, действительно,

.

Дата добавления: 2014-01-07