Основные теоремы о пределах функций

Теоремы о пределах функций

Лекция 13.

Основные теоремы о пределах функций. Замечательные пределы.

Теорема 1. Функция у = у(х) не может иметь более одного предела при х→.

Доказательство. Предположим противное, пусть функция у = у(х) при х→имеет два предела А₁≠А₂. По свойствам бесконечно малых функций у(х)=А₁ + a₁(х) и у(х)=А₂+a₂(х), где a₁(х), a₂(х) ─ б.м.ф. при х→. Тогда А₁ + a₁(х) = А₂ + a₂(х) или А₁ – А₂ = a₁(х) – a₂(х). Но последнее равенство невозможно, т.к. в левой части стоит постоянная, отличная от нуля, а в правой ─ бесконечно малая функция.

Теорема 2. Если каждая из функций у = у(х), z = z(x) имеет предел при х→, то сумма, разность, произведение этих функций также имеют пределы, причём

1) (у(х) ± z(x)) = y(x) ± z(x);

2) (y(x) × z(x)) = y(x) × z(x),

если кроме того, z(x) ≠ 0, то частное имеет предел, причём

3) = .

Доказательство. Пусть y(x) = А, z(x) = В.

Тогда по свойствам б.м.ф. у(х)=А + a(х), z(x) = B + b(x), где a(х), b(х) ─ б.м.ф. при х→. Получаем:

1) у(х) ± z(x) = (А ± В) + (a(х) ± b(х)). По свойствам б.м.ф. a(х) ± b(х) ─ б.м.ф., поэтому (у(х) ± z(x)) = А ± В, т.е. (у(х) ± z(x)) = y(x) ± z(x).

2) y(x) × z(x) = (А + B + b(x) = А×В + a(х) ×B + А× b(x) + a(х)×b(x). По свойствам б.м.ф. функция a(х) ×B + А× b(x) + a(х)×b(x) ─ б.м.ф. при х→.

Поэтому (y(x) × z(x)) = АВ = y(x) × z(x).

3) Пусть В≠0. Рассмотрим разность

− .

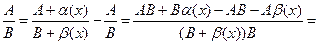
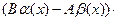
По свойствам б.м.ф. функция ─ б.м.ф. при х→.

Рассмотрим функцию =.

Очевидно, что =.

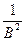Это означает, что для e, равного, например, найдутся х, расположенные вокруг такие, что │−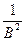│< , т.е.

−<−<, <<.

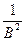Но это означает, что функция ограничена. Тогда по свойствам б.м.ф. произведение

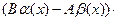
─ б.м.ф. при х→.

Обозначим её a₁(х), т.е. 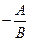= a₁(х). Тогда + a₁(х). По свойствам б.м.ф. = = .

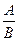Следствие 1. Постоянный множитель можно выносить за знак прела, т.е. если

с = const, то (с×у(х)) = су(х).

Следствие 2. Если у(х) = А, то для любого натурального числа m

(у(х))^m = (у(х))^m = A^m.

Теорема 3. Пусть три функции u = u(x), v = v(x), y = y(x) определены в некотором промежутке, содержащем точку . Если для любого х из этого промежутка выполняется неравенства

u(x) £ y(x) £ v(x)

и функции u = u(x), v = v(x) имеют одинаковые пределы при х→, то функция у = у(х) имеет тот же предел при х→.

Доказательство. Пусть u(x) = v(x) = A.

Т.к. u(x) £ y(x) £ v(x), то u(x)−А £ y(x)−А £ v(x)−А.

По определению предела функции "e>0 существуют d₁>0 и d₂>0 такие, что из неравенств 0<│х − │<d₁ следует │u(x)−A│<e, а из неравенств 0<│х − │<d₂ следует │v(x)−A│<e. Обозначим d = min{d₁,d₂}. Тогда для х, удовлетворяющих неравенствам 0<│х − │<d следует −e < u(x)−A < e и −e < v(x)−A < e. Поэтому из неравенств u(x)−А £ y(x)−А £ v(x)−А следует −e < у(x)−A < e, т.е. │у(x)−A│<e. Это означает, что у(х) = А.

Теорема 4. Пусть функция у = f(x) определена в некотором промежутке, содержащем точку . Если при х→функция у = f(x) имеет положительный (отрицательный) предел, то найдётся такой промежуток вокруг точки , что для всех х из этого промежутка функция положительна (отрицательна).

Доказательство. Пусть f(x) = А. Это означает, что "e>0 можно указать такое число d>0, что при всех х, удовлетворяющих условию 0<│х−│<d, выполняется

Неравенство │f(x)−A│<e, т.е. −e < f(x)−A < e.

Если А>0, то взяв e = А из неравенства A− e <f(x) получим f(x)>A−e= =A− A = A>0, т.е. f(x)>0 при −d<x−<d, т.е. при −d<x<d+.

Если А<0, то взяв e = −А, из неравенства f(x)< A+e получим f(x)< A+e = =A− A = A<0, т.е. f(x)<0 при −d<x<d+.

Эта теорема называется теоремой о сохранении знака функции, имеющей предел.

Теорема 5. Если функции u(x), v(x) определены в некотором промежутке, содержащем точку , и для всех х из этого промежутка, кроме х=, выполняется неравенство u(x)<v(x), причём функции u(x) и v(x) имеют пределы при х→. Тогда u(x) £ v(x).

Доказательство. Пусть u(x) = А, v(x) = В. Положим, что А>B. По теореме2 (u(x)−v(x)) = А−В>0. По теореме 4 найдётся промежуток вокруг точки такой, что для всех х из этого промежутка u(x)−v(x)>0, т.е. u(x)>v(x), что противоречит условию.

Следовательно, предположение неверно и А£В, т.е. u(x)£ v(x).

Дата добавления: 2014-01-07