Производная и дифференциал функций

Лекция 15.

Пример 3.

f(x) = 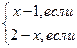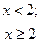х₀ = 0 является точкой устранимого разрыва первого рода.

Положив g(x) = 1 при х = 0, разрыв устранится, функция станет непрерывной.

Производная и дифференциал функции. Правила дифференцирования.

Определение. Пусть на некотором промежутке (а;b) определена функция у=f(x). Возьмём произвольную точку х₀Î(а;b) и придадим аргументу х в точке х₀ произвольное приращение ∆х токое, что точка х₀ + ∆хÎ(а;b). Производной функции у = f(x) в точке х₀ называется предел при ∆х→0 отношения приращения функции в этой точке к приращению аргумента, если этот предел существует. Обозначается предел функции f(x) в точке х₀ через f '(x₀), т.е.

f '(x₀) = =.

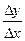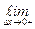
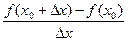Если функция у=f(x) имеет конечную производную в каждой точке хÎ(а;b), то производную f '(x) можно рассматривать как функцию от х, определённую на (а;b).

Если для некоторого значения х₀ выполняется условие

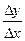= + ∞ (или = − ∞),

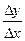то говорят, что в точке х₀ функция f(x) имеет бесконечную производную знака плюс (или знака минус).

Пример. Найти производную функции f(x) = x² в точке х = х₀.

Решение. Придавая аргументу х в точке х₀ приращение ∆х, находим

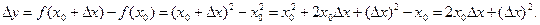
Тогда =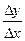

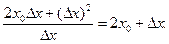
Теперь находим f '() = =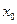

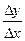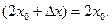
Таким образом можно составить таблицу производных простейших элементарных функций:

1. (C)' = 0, где С = const;

2. ()' = 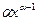. В частности ,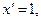

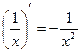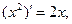
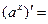
3. 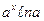. В частности, .

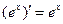4. 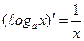×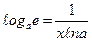. В частности,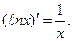

5.

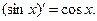
6.

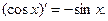
7. (tg)'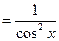. 10. .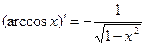

8. (ctg)'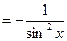. 11. (arctg)'.

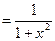9. 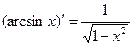. 12. (arcctg)'.

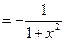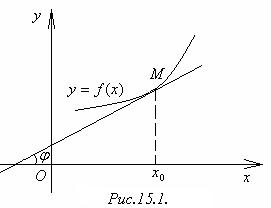Из школьного курса математики известно: геометрический смысл производной состоит в том, что производная функции f(x) в точке х₀ равна угловому коэффициенту касательной к графику функции f(x) в точке М(х₀;f(x₀)), т.е.

f '(x₀) = tgφ (рис.15.1).

Пример. Составить уравнение касательной, проведённой из точки М(1;−3) к параболе f(x) = x².

Решение. Пусть касательная в точке (х₀;f(x₀)) к параболе f(x)=x² имеет уравнение у=kx+b. Тогда по геометрическому смыслу касательной k = f '(x₀) = 2x₀. Так как касательная проходит через точки (1;−3) и (х₀;х₀²), то имеем систему:

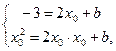
откуда, вычитая из второго уравнения первое, получим

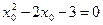
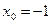или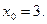

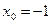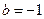Если , то и уравнение касательной имеет вид у = .

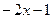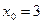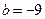Если , то и уравнение касательной ─ у = .

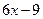Определение. Функция у = f(x) называется дифференцируемой в точке х₀, если она имеет в этой точке конечную производную. Если функция дифференцируема в каждой точке интервала (а;b), то она называется дифференцируемой на (а;b).

В связи с этим определением операцию нахождения производной часто называют дифференцированием.

Если функция у = f(x) дифференцируема в точке х₀, то справедливы следующие утверждения:

1) ∆у = А×∆х + α(∆х)∆х, где ∆х ─ приращение аргумента, ∆у ─ приращение функции, А ─

число, не зависящее от ∆х, α(∆х) ─ бесконечно малая функция при ∆х→0.

Очевидно, что А = 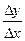= f '(x₀).

2) функция у = f(x) непрерывна в точке х₀.

Однако, не всякая непрерывная функция является дифференцируемой. Например, функция у = 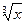непрерывна в точке х₀ = 0, т.к. 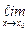f(x) =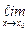 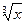= 0 = f(x₀).

Однако производная у' = (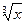)'= 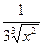в точке х₀ = 0 не существует, т.е. функция в точке х₀ = 0 не дифференцируема.

Определение. Пусть функция у = f(x) дифференцируема в точке х₀. Дифференциалом функции f(x) в точке х₀ называется часть приращения функции

dy = f '(x₀)×∆x.

Дифференциалом независимой переменной х называется приращение этой переменной, т.е. dx = ∆x. Таким образом,

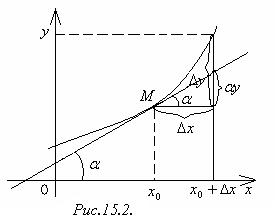Геометрический смысл дифференциала функции у = f(x) состоит в том, что дифференциал dy в точке х₀ равен приращению ординаты касательной к графику этой функции в точке М(х₀;f(x₀)) (рис.15.2).

Во многих задачах приращение функции в данной точке можно приближённо заменить дифференциалом функции в этой точке: ∆у» dy.

Пример. Используя дифференциал функции, вычислить приближённо .

Решение. Пусть функция у = 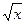. Положим 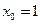и приращение аргумента . Тогда

∆у = 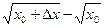» dy = y'.

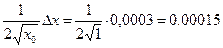Теперь » 1+ 0,00015 = 1,00015.

Правила дифференцирования функций сформулируем в следующей теореме.

Теорема 1. Если функции u = u(x) и v = v(x) дифференцируемы в точке х₀, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x₀)≠0) также дифференцируемы в этой точке, причём имеют место следующие формулы:

1) ;

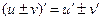2) ;

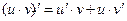3) .

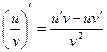Дата добавления: 2014-01-07