Примеры. Понятие о первообразной функции

Понятие о первообразной функции.

Лекция 18.

Неопределённый интеграл и его свойства

Понятие о первообразной функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов. Понятие об основных методах интегрирования.

Рассмотрим задачу, обратную задаче о дифференцировании функций, т.е. задачу о восстановлении функции F(x) по известной её производной f(x).

Определение. Функция F(x), определённая в промежутке (а;b), называется первообразной данной функции f(x) в этом промежутке, если для любого значения хÎ(а;b) выполняется равенство F'(x) = f(x).

1. F(x) = sinx является первообразной функции f(x) = cosx.

2. F(x) = x³ является первообразной для функции f(х) = 3х².

Теорема 1. Если F(x) ─ первообразная функции f(x), то множество

{F(x) + CôC ─ произвольная постоянная}

есть множество всех первообразных функции f(x).

Доказательство. Очевидно, что любая функция Ф(х) = F(x) + C₀, где С₀ ─ некоторая постоянная, является первообразной функции f(x), т.к. Ф'(х)= (F(x) + C₀)' = F'(x) + C'₀= f(x). Обратно, если Ф(х) ─ некоторая первообразная функции f(x), то

(Ф(х) – F(x))' = Ф'(х) – F'(x) = f(x) – f(x) = 0. Но это означает, что функция Ф(х) – F(x) постоянна, т.е. существует произвольная постоянна С₁ такая, что Ф(х) – F(x) = С_1, откуда Ф(х) = F(x) + С₁.

18.2. Неопределённый интеграл и его свойства.

Определение. Если функция F(x) ─ первообразная функции f(x), то множество всех функций F(x) + С, где С ─ произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается

ò f(x)dx = F(x) + C.

При этом функция f(x) называется подинтегральной функцией, f(x)dx ─ подинтегральным выражением. Операция нахождения неопределённого интеграла называется также интегрированием.

Свойство 1. Производная неопределённого интеграла равна подинтегральной функции; дифференциал от неопределённого интеграла равен подинтегральному выражению, т.е.

(ò f(x)dx)' = f(x); d(ò f(x)dx) = f(x)dx.

Свойство 2. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

ò d(j(x)) = j(x) + С.

Свойство 3. Постоянный множитель можно выносить за знак неопределённого интеграла, т.е.

ò k×f(x)dx = k×ò f(x)dx (k = const, k¹0).

Свойство 4. Если функции f₁(x) и f₂(x) имеют первообразные, то функция f₁(x) + f₂(x) также имеет первообразную, причём

ò (f₁(x) + f₂(x))dx = ò f₁(x)dx + ò f₂(x)dx.

Свойство 4.1. Если функции f₁(x), f₂(x),…, f_n(x) имеют первообразные, то функция

f₁(x) + f₂(x) +…+ f_n(x) также имеет первообразную, причём

ò (f₁(x) +…+ f_n(x))dx = ò f₁(x)dx + … +ò f_n(x)dx..

18.3. Таблица основных неопределённых интегралов.

1. ò dx = x + C, 6. ò cosxdx = sinx + C,

1. ò x^adx = 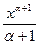+ C,(a > 0) 7.ò sinxdx = - cosx + C,

1. ò dx = ℓnôxô+ C, 8. ò 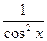dx = tgx + C,

1. ò a^xdx = + C, (a > 0) 9. ò 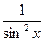dx = - ctgx + C,

1. ò e^xdx = e^x + C, 10. ò 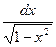=arcsinx + C =-arccosx+ C

11. ò dx = arctgx + C = - arcctgx + C.

Замечание. Формулы этой таблицы остаются справедливыми и в случае, когда вместо х поставить некоторую дифференцируемую функцию u = u(x), т.е. можно записать обобщённую таблицу простейших неопределённых интегралов:

1. ò du = u + C, 2. ò u^adu = 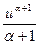+ C (a ¹ 1)

и т.д.

Дата добавления: 2014-01-07