Свойства определенного интеграла

Задача о площади криволинейной трапеции.

Лекция 19.

Определённый интеграл и его приложения

Задача о площади криволинейной трапеции. Понятие определённого интеграла. Свойства определенного интеграла. Теорема об оценке определённого интеграла. Теорема о среднем. Определённый интеграл с переменным верхним пределом, его свойства. Формула Ньютона-Лейбница. Основные методы интегрирования. Приложения определённого интеграла.

Рассмотрим криволинейную трапецию 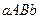(рис.19.1), т.е. плоскую фигуру, ограниченную сверху графиком функции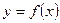(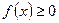), слева и справа ─ отрезкам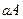и и 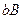прямых , снизу - осью .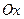

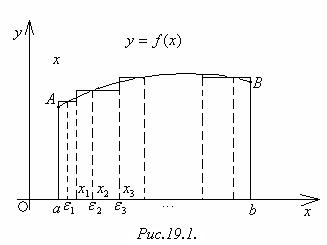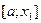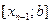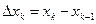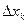Отрезок [] точками =разобьём на n элементарных отрезков , , …, , длины которых обозначим через для k=1,2,…,n. В каждом элементарном отрезке выберем произвольную точку и вычислим в ней значение данной функции f(). Произведение f()выражает площадь прямоугольника с основанием 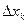и высотой f().

Составим сумму всех таких произведений

S_n = (1)

Эта сумма называется интегральной суммой для функции 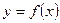на [] и выражает площадь ступенчатой фигуры, состоящей из прямоугольников и приближённо заменяющей данную трапецию. Очевидно, что сумма S_k зависит от способа разбиения и выбора точек .

Обозначим через λ длину наибольшего из элементарных отрезков , k=1,2,…,n, т.е. λ=max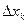. Число S, вычисляемое по формуле

S = 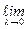S_n = ,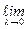

называется площадью криволинейной трапеции.

19.2. Понятие определённого интеграла.

Пусть дана функция 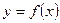, определённая на [], где 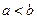. Отрезок [] точками =разобьём на n элементарных отрезков 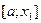, , …, , 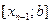длины которых обозначим через 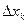, т.е. 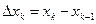, k=1,2,…,n. В каждом из элементарных отрезков выберем произвольно одну точку , значение функции f() умножим на длину отрезка 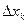и составим сумму всех таких произведений

S_n = (2)

Сумма (2) называется интегральной суммой для функции 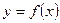на [].

Обозначим через λ длину наибольшего из элементарных отрезков , т.е.

λ=max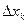, k=1,2,…,n.

Определение. Определённым интегралом от функции 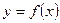на [] называется, конечный предел её интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю.

Обозначается: . 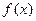называется подинтегральной функцией, ─ переменной интегрирования, ─ нижним пределом интегрирования, 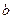─ верхним пределом интегрирования.

Следовательно, по определению

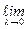
= (3)

Из определения следует, что величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.

= = … = .

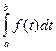Функция, для которой существует предел (3), называется интегрируемой на [].

Геометрический смысл определённого интеграла состоит в том, что если 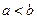и f(x)≥0, то определённый интеграл от функции 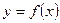по отрезку [] равен площади криволинейной трапеции, ограниченной сверху графиком функции 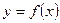, слева и справа прямыми , снизу - осью .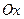

3.1. По определению полагаем

= 0.

3.2. при перестановке пределов интегрирования определённый интеграл меняет знак на противоположный, т.е.

= −.

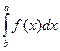3.3. Свойство аддитивности.

Если промежуток интегрирования [] разбит на конечное число отрезков 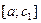, , …, , 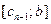то

= + + … + .

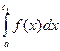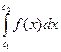3.4. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

= .

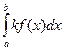3.5. Определённый интеграл от алгебраической суммы конечного числа интегрируемых функций равен алгебраической сумме интегралов от этих функций,

= +…+ .

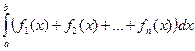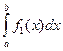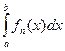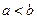3.6. если функция интегрируема на [], где , и ≥0 для всех [], то

≥ 0.

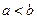3.7. Если функции , φ(x) интегрируемы на [], где , и ≤ φ(x) для всех [], то

≤ .

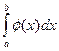3.8. Если функция интегрируема на [], где 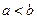, то функция ││ также интегрируема на [], причём

.

19.4. Теорема об оценке определённого интеграла. Теорема о среднем.

Теорема (об оценке определённого интеграла).

Если функция интегрируема на отрезке [], где 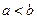, и для всех [] выполняется неравенство

m ≤ ≤ M,

то

m≤ ≤ M. (*)

Доказательство. На основании свойства 3.7 из неравенства m ≤ f(x) ≤ M находим, что

≤ ≤ .

Из свойства 3.4 имеем

≤ ≤ .

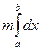Покажем, что 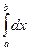=. Действительно,

= = = .

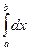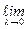
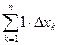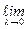
Теперь получаем

m≤ ≤ M.

Теорема доказана.

Неравенство (*) позволяет оценить определённый интеграл, т.е. указать границы, между которыми заключено его значение.

Пример. Оценить определённый интеграл .

В данном случае 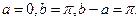Так как 3 ≤ 3+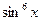≤ 4, то 3π ≤≤ 4π.

Дата добавления: 2014-01-07