
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема (о среднем значении)
|
|
|
|
Если функция  непрерывна на отрезке [
непрерывна на отрезке [ ], то на этом отрезке существует точка
], то на этом отрезке существует точка  такая, что
такая, что
 =
=  (**)
(**)
Формула (**) называется формулой среднего значения.
Доказательство. Так как функция  непрерывна на [
непрерывна на [ ], то по второй теореме Вейерштрасса, существует числа m и M такие, что
], то по второй теореме Вейерштрасса, существует числа m и M такие, что
 f(x) = m ≤
f(x) = m ≤  ≤ M =
≤ M = 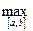 f(x).
f(x).
Тогда по теореме об оценке определённого интеграла находим
m ≤
≤  ≤ M
≤ M
и следовательно,
m ≤ 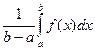 ≤ M.
≤ M.
Положим 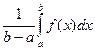 = μ, (m ≤ μ ≤ M).
= μ, (m ≤ μ ≤ M).
Так как μ заключено между наименьшим и наибольшим значениями непрерывной функции  на [
на [ ], то, учитывая вторую теорему Больцано-Коши, можем указать точку
], то, учитывая вторую теорему Больцано-Коши, можем указать точку  [
[ ] такую, что
] такую, что  = μ.
= μ.
Таким образом,
 =
=  .
.
Теорема доказана.
19.5. Определённый интеграл с переменным верхним пределом, его свойства. Формула Ньютона-Лейбница.
Рассмотрим функцию 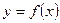 , интегрируемую на [
, интегрируемую на [ ]. Если
]. Если  [
[ ], то функция f(x) интегрируема также на любом отрезке [
], то функция f(x) интегрируема также на любом отрезке [ ]. Предположим, что
]. Предположим, что  меняется на [
меняется на [ ], тогда на этом интеграле определена функция
], тогда на этом интеграле определена функция
Ф( ) =
) = 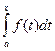 ,
,
Где  ─ переменная интегрирования,
─ переменная интегрирования,  ─ переменный верхний предел. Эту функцию называют определённым интегралом с переменным верхним пределом.
─ переменный верхний предел. Эту функцию называют определённым интегралом с переменным верхним пределом.
Свойство 1. Определённый интеграл с переменным верхним пределом является непрерывной на [ ] функцией.
] функцией.
Свойство 2. Если подинтегральная функция  непрерывна, то производная определённого интеграла с переменным верхним пределом существует и равна значению подинтегральной функции для этого предела интегрирования, т.е.
непрерывна, то производная определённого интеграла с переменным верхним пределом существует и равна значению подинтегральной функции для этого предела интегрирования, т.е.
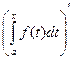 = f(x).
= f(x).
Следствие. Определённый интеграл с переменным верхним пределом является одной из первообразных для непрерывной подинтегральной функцией, т.е. для любой непрерывной функции существует производная.
Связь между определённым и неопределённым интегралами выражает следующая теорема.
Теорема (о формуле Ньютона-Лейбница).
Пусть функция  непрерывна на отрезке [
непрерывна на отрезке [ ]. Тогда, если функция F(x) является некоторой её первообразной на этом отрезке, то справедлива следующая формула
]. Тогда, если функция F(x) является некоторой её первообразной на этом отрезке, то справедлива следующая формула
 = F(
= F(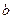 ) – F(
) – F( ).
).
Эта формула называется формулой Ньютона-Лейбница.
Доказательство. Пусть Ф(х) является первообразной для функции  на [
на [ ]. Пусть F(x) ─ некоторая постоянная. Подставим в последнее равенство
]. Пусть F(x) ─ некоторая постоянная. Подставим в последнее равенство 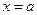 .
.
Тогда
 = F(
= F( ) + C,
) + C,
т.е. О = F( ) + C, откуда С = − F(
) + C, откуда С = − F( ).
).
Итак, для любого  [
[ ]
]  = F(
= F( ) – F(
) – F( ).
).
Полагая  , получим
, получим  = F(
= F(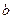 ) – F(
) – F( ).
).
Теорема доказана.
Разность F(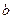 ) – F(
) – F( ) принято условно записывать в виде F(
) принято условно записывать в виде F( )
)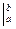 . Тогда формула Ньютона-Лейбница принимает вид
. Тогда формула Ньютона-Лейбница принимает вид
 = F(
= F( )
)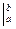 .
.
Эта формула не только устанавливает связь между определённым и неопределённым интегралами, но и даёт простой метод вычисления определённого интеграла.
Пример.  =
= 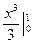 =
= .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 883; Нарушение авторских прав?; Мы поможем в написании вашей работы!