Степенные ряды

Определение. Степенным рядом называется функциональный ряд вида

, (1)

где - действительные числа, называемые коэффициентами степенного ряда.

А) Если степенной ряд сходится лишь в точке 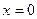, то он относится к рядам первого класса.

Например, ряд

(2)

относится к рядам первого класса. Зафиксируем и рассмотрим числовой ряд

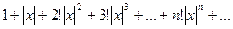
По признаку Даламбера

= =

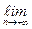
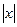
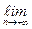
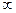
и ряд расходится при всех . Следовательно, ряд (2) сходится только при .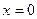

Б) Если ряд (1) сходится на всей числовой прямой, то он относится к рядам второго класса.

Например, применив признак Даламбера при фиксированном нетрудно убедится, что к рядам второго класса относится ряд

В) Ряд (1), не принадлежит первому и второму классам, относят к рядам третьего класса.

Теорема Абеля. Если степенной ряд (1) сходится при , то он абсолютно сходится для любого , удовлетворяющего условию

;

если же степенной ряд (1) расходится при 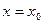, то он расходится и при любом , удовлетворяющем условию .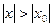

Следствие. Для каждого степенного ряда (1) третьего класса существует число , называемое радиусом сходимости этого ряда, для которого выполняется условия: при ряд (1) сходится абсолютно, при ряд (1) расходится.

Промежуток называется интервалом сходимости степенного ряда. Для степенного ряда (1) второго класса интервал сходимости .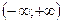

Областью сходимости степенного ряда (1) является интервал , к которому в отдельных случаях добавляется один или оба конца этого интервала (это исследуется для конкретных рядом при и ).

Для степенного ряда (1) первого класса полагают ; для степенного ряда (1) второго класса .

Теорема 2. Пусть для степенного ряда (1) существует и отличен от нуля предел

.

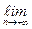
Тогда .

Пример 10. Найти область сходимости степенного ряда .

Решение. = .

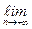
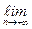
Рассмотрим = = 5. Тогда . Итак, - интервал сходимости.

Исследуем ряд на концах интервала.

а) . Имеем ряд ==.

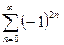Этот ряд расходится согласно необходимого признака сходимости рядов.

б) . Имеем ряд = .

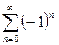Тогда

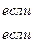
Поэтому 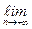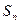не существует и ряд 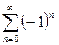расходится.

Итак, область сходимости ряда .

Дата добавления: 2014-01-07