План лекции. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С

Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания

Контрольные задания для СРС – 1) доказать самостоятельно простейшие теоремы статики; 2) указать отличие цилиндрического шарнира от сферического; 3) смысл принципа освобождаемости от связей; 4) может ли одна и та же сила в одном случае быть внешней, а в другом - внутренней? 5) три силы, действующие на тело, находятся в равновесии. Можно ли утверждать, что их линии действия пересекаются в одной точке?

Лекция 2. Моменты силы относительно точки и оси. Пары сил

Цель лекции – изложить основные понятия и теоремы о моментах сил и парах сил.

1. Моменты силы относительно точки и оси

2. Теория пар сил

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Моментом силы относительно точки называют вектор, приложенный в этой точке, равный по величине произведению модуля силы на плечо силы относительно этой точки и направленный перпендикулярно к плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть силу стремящейся вращать тело против хода часовой стрелки.Точку, относительно которой определен момент силы, называют моментной точкой. Проведенный из моментной точки перпендикуляр к линии действия силы называется плечом силы.

Для плоской системы сил используется алгебраический момент силы относительно точки, равный алгебраической величине произведения модуля силы на плечо силы относительно этой точки. Знак момента силы определяется по следующему правилу: момент считается положительным, если сила стремится повернуть тело вокруг точки против хода часовой стрелки, если по ходу часовой стрелки – отрицательным.

.

Отметим следующие свойства момента силы относительно точки:

1) момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, так как при этом не меняется плечо силы;

2) момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку (плечо силы равно нулю).

Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью.

Чтобы определить момент силы относительно оси необходимо:

1) провести через произвольную точку О оси плоскость П, перпендикулярную оси;

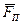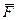2) найти проекцию силы на плоскость П;

3) определить плечо h силы 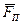относительно точки О;

4) вычислить произведение ;

5) определить знак момента: принимаем его со знаком плюс, если с положительного конца оси поворот, который стремится совершить сила 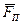, виден против хода часовой стрелки, и со знаком минус – если по ходу часовой стрелки (рис.3)

.

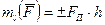Момент силы относительно оси равен нулю: 1) если сила параллельна заданной оси; 2) если линия действия силы пересекает ось.

Теорема о зависимости между моментом силы относительно оси и моментом силы относительно точки на оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.

Парой сил называется система двух равных по величине сил, направленных по параллельным прямым в противоположные стороны. Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил. Плоскость, в которой действуют силы пары, называется плоскостью действия пары сил. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара сил не приводится к равнодействующей силе. Действие пары на твердое тело сводится к вращательному эффекту, мерой которого является векторная величина, называемая моментом пары сил. Модуль этого вектора равен произведению модуля силы пары на ее плечо, т.е.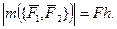

Основные свойства пары сил: 1) пару сил можно переносить в любое место в плоскости действия пары; 2) пару сил можно переносить в любую плоскость, параллельную данной; 3) можно произвольно менять величину силы и плечо пары сил, сохраняя неизменным ее момент.

Пары сил эквивалентны, если равны векторы-моменты этих пар. Если на тело действует несколько пар с моментами 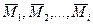, то их можно привести к одной паре сил с моментом .

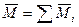ГЛОССАРИЙ

Нүктеге қатысты күш моментi	Момент силы относительно точки	Moment of force about point
Өске қатысты күш моментi	Момент силы относительно оси	Moment of force about axis
Күш иiнi	Плечо силы	Moment arm
Қос күш	Пара сил	Couple
Қос күш иiнi	Плечо пары	Arm of couple
Қос күш моментi	Момент пары	Moment of couple

Рекомендуемая литература

1. Яблонский А.А. Курс теоретической механики. Ч. 1, «Высшая школа», С-Птб.: 2002 и предшествующие издания.

Дата добавления: 2014-01-07