План лекции. 1. Теорема о скоростях точек плоской фигуры

1. Теорема о скоростях точек плоской фигуры.

2. Теорема об ускорениях точек плоской фигуры.

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Плоским движением твердого тела называется такое движение, при котором каждая его точка движется в одной и той же плоскости, параллельной данной неподвижной плоскости.

Плоское движение часто встречается в технике. Большинство современных механизмов имеет звенья, совершающие плоские движения. Такие механизмы называются плоскими.

Уравнения

,

определяющие положение и движение плоской фигуры в неподвижной плоскости Оxy, называются уравнениями плоского движения твердого тела.

Введем понятия алгебраической угловой скорости 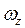и алгебраического углового ускорения 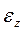твердого тела в плоскопараллельном движении:

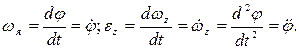
Для произвольного момента времени скорость точки твердого тела будет определяться следующей формулой:

где - скорость точки А, выбранной за полюс; - скорость точки В тела при вращении ее вместе с фигурой вокруг полюса А. Вектор лежит в плоскости движущейся фигуры и 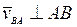. Вектор , его модуль: .

Окончательно имеем:

.

Таким образом, скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса и скорости этой точки при ее вращении вместе с фигурой вокруг полюса.

Для определения ускорений точек плоской фигуры необходимо пользоваться следующей формулой:

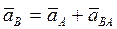
Здесь - ускорения точек В и А относительно неподвижной системы координат; - ускорение точки В при ее вращательном движении вместе с плоской фигурой вокруг подвижной оси, проходящей через полюс А.

Таким образом, ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при ее вращательном движении вместе с плоской фигурой вокруг полюса.

Учитывая, что 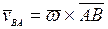найдем:

,

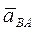
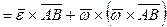где 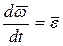- угловое ускорение тела при плоском движении. Слагаемые вектора 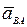есть касательная и нормальная составляющие:

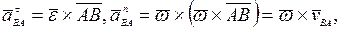
модули которых равны:

.

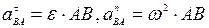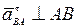, вектор 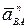направлен от В к полюсу А..

Таким образом,

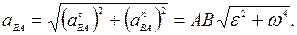
ГЛОССАРИЙ

Қатты денеiң жазық-параллель қозғалысы	Плоско-параллельное движение твердого тела	Two-dimensional motion of rigid body
Лездiк жылдамдықтар центрi	Мгновенный центр скоростей	Instantaneous centre of zero-velocity
Лездiк үдеулер центрi	Мгновенный центр ускорений	Instantaneous centre of zero-acceleration
Қозғалмалы центроида	Подвижная центроида	Body cent rode
қозғалмайтын центроида	Неподвижная центроида	Space cent rode

Рекомендуемая литература

1. Яблонский А.А. Курс теоретической механики. Ч. 1, «Высшая школа», С-Птб.: 2002 и предшествующие издания.

Дата добавления: 2014-01-07