План лекции. Системы. Теорема о движении центра масс системы

Системы. Теорема о движении центра масс системы

Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания

Контрольные задания для СРС - доказать самостоятельно теорему Штейнера-Гюйгенса. Применить ее к простейшим однородным телам.

Лекция 11. Дифференциальные уравнения движения механической

Цель лекции – рассмотреть дифференциальные уравнения движения механической системы и теорему о движении центра масс системы.

Дифференциальные уравнения движения механической системы

Теорема о движении центра масс механической системы

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Рассмотрим движение механической системы, состоящей из N точек. На точку M_k массой m_k системы действует равнодействующая внутренних сил 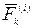и равнодействующая внешних сил .

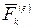Дифференциальные уравнения движения системы материальных точек в векторной форме имеют вид:

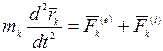или ,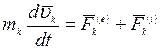

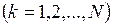где 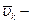скорость k – ой точки.

Начальные условия имеют следующий вид:

при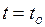

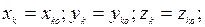
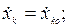
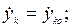
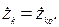
Проинтегрировать систему 3 N уравнений в общем случае не удается даже для одной точки. Процесс интегрирования еще более усложняет то обстоятельство, что силы реакций связей, наложенных на систему, часто необходимо определять в процессе решения задачи о движении механической системы.

Для решения некоторых задач необходимо систему уравнений преобразовать так, чтобы в них содержались зависимости некоторых обобщенных мер движения (количества движения, кинетического момента, кинетической энергии) от характеристик приложенных сил (главного вектора и главного момента относительно центра). Получают эти уравнения из закономерностей, описываемых общими теоремами динамики для механической системы: о движении центра масс, об изменении количества движения, об изменении кинетического момента, об изменении кинетической энергии.

Запишем уравнения движения механической системы в виде

,

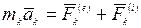
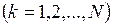где 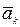- ускорение 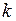- ой точки; 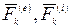- равнодействующие внешних и внутренних сил, действующих на 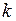- ую точку. Просуммируем уравнения по всем точкам механической системы:

.

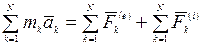Здесь 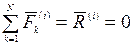- главный вектор внутренних сил.

Продифференцировав дважды по времени выражение для определения радиус-вектора центра масс системы:

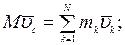
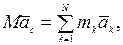
где 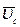- абсолютная скорость центра масс.

Тогда

,

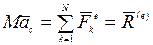где 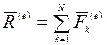- главный вектор внешних сил, действующих на механическую систему.

Теорема о движении центра масс механической системы формулируется так: центр масс механической системы движется так же, как и материальная точка, масса которой равна массе всей системы и на которую действуют все внешние силы, действующие на точки системы.

Из теоремы о движении центра масс вытекает следующее следствие (закон сохранения движения центра масс):

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. 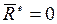, то 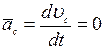, откуда после интегрирования получаем: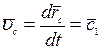

Таким образом, если главный вектор внешних сил, действующих на механическую систему, равен нулю, то центр масс механической системы движется прямолинейно и равномерно.

ГЛОССАРИЙ

Механикалық жүйе	Механическая система	System
Механикалық жүйесiнiң массалар центрi	Центр масс механической системы	Center of mass

Рекомендуемая литература

1. Яблонский А.А. Курс теоретической механики. Ч. 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.

Дата добавления: 2014-01-07