План лекции. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С

Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания

Контрольные задания для СРС – 1) Влияют ли внутренние силы системы на изменение ее кинетической энергии? 2) В каких механических системах сумма работ внутренних сил равна нулю?

Лекция 14. Теорема об изменении количества движения

Цель лекции - изложить теорему об изменении количества движения для материальной точки и механической системы

Количество движения материальной точки и механической системы. Элементарный и полный импульс силы

Теорема об изменении количества движения

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости

.

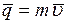Количеством движения механической системы называется вектор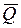, равный геометрической сумме количеств движения всех точек системы:

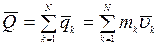
Вектор 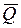является свободным вектором. Единица измерения в системе СИ – 1 кг ∙м/с. Используя понятие центра масс механической системы, количество движения системы представим в виде:

.

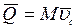Элементарным импульсом силы за элементарный промежуток времени 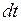называется векторная величина, равная

.

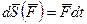Полный импульс силы 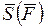за конечный промежуток времени 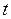равен:

.

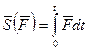Единица измерения импульса силы – Ньютон ∙ секунда (Н∙ с).

,

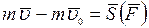где 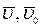- конечная и начальная скорости точки; 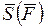- полный импульс силы за время 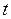. Это уравнение выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы за этот же промежуток времени.

Для механической системы будем иметь:

.

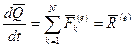Это уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.

Умножая обе части уравнения на dt, получим:

,

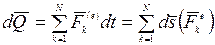т.е., дифференциал количества движения механической системы равен геометрической сумме элементарных импульсов всех внешних сил, действующих на систему.

Интегрируя уравнение в заданных пределах, получим:

,

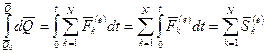или

,

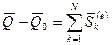где 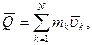- количества движения системы в начальный и конечный моменты времени.

Последнее уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему, за это же время.

Теорема допускает первый интеграл (закон сохранения) в случае, если геометрическая сумма всех внешних сил равна нулю:

.

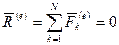Тогда вектор количества движения системы будет постоянен по модулю и по направлению: .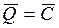

ГЛОССАРИЙ

Нүктенiң (жүйенiң) қозғалыс мөлшерi	Количество движения точки (системы)	Momentum of particle (system)
Қандай да бiр уақыт аралығындағы күш импульсi	Импульс силы за конечный промежуток времени	Whole force

Рекомендуемая литература

1. Яблонский А.А. Курс теоретической механики. Ч 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.

Дата добавления: 2014-01-07