Пример. Рассмотрим реакцию

C_{(графит)} + O_2(газ) → CO_2(газ); тепловой эффект реакции равен ∆H₁.

Запишем реакцию через промежуточные стадии.

C_{(графит)} + 0,5O_2(газ) = CO_(газ), ∆H₂ ; (1)

CO_(газ) + 0,5O_2(газ) = CO_2(газ), ∆H₃; (2)

Просуммируем реакции (1) и (2):

C_{(графит)} + O_2(газ) → CO_2(газ).

Получаем исходную реакцию, поэтому сумма тепловых эффектов реакций (1) и (2) равна тепловому эффекту исходной реакции: ∆H₂ + ∆H₃ = ∆H₁.

Условие применения закона Гесса: закон применим только к тепловым эффектам процесса,т.е. к условиям, когда процесс протекает при Р=const или V=const, а полезная работа равна нулю = 0, температура продуктов реакции равна температуре исходных веществ. Закон применим не только к химическим реакциям, но и к любым другим физико-химическим процессам.

Пример: ∆H _{возгонки} = ∆H _плвл + ∆H _испар.

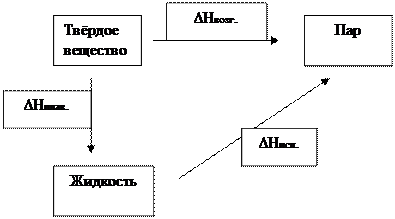
Термодинамическое обоснование закона Гесса заключается в следующем. Установлено, что Q_V = ∆U, а Q_P = ∆Н. Так как внутренняя энергия U и энтальпия H являются функциями состояния системы, т. е. не зависят от пути процесса, то Q_V и Q_P не будут зависеть от промежуточных стадий, а определяются только начальным и конечным состоянием системы.

Практическое значение закона Гесса заключается в следующем. Закон позволяет рассчитывать тепловые эффекты процессов не проводя экспериментов; тепловые эффекты неосуществимых процессов и процессов, для которых тепловой эффект нельзя определить опытным путём.

Уравнение химической реакции с указанием теплового эффекта называется термохимическим уравнением. С термохимическими уравнениями можно обращаться также, как и с алгебраическими уравнениями (складывать, умножать, делить).

Первое следствие из закона Гесса: тепловой эффект обратной реакции равен по величине и противоположен по знаку тепловому эффекту прямой реакции.

.

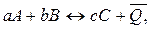
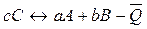Второе следствие из закона Гесса: тепловой эффект реакции равен сумме теплот (энтальпий) образований продуктов реакций за вычетом (минус) суммы теплот (энтальпий) образования исходных веществ.

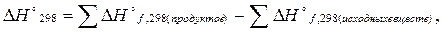
здесь индекс f от лат. foramentum – образование.

Например для реакции aA + bB→cC + dD,

∆Hº ₂₉₈ = (с∆Hº_{f, 298 (C)} + d∆Hº_{f, 298 (D)}) – (a∆Hº_{f, 298 (A)} + b∆Hº_{f, 298 (B)}).

При суммировании обязательно учитываются стехиометрические коэффициенты уравнения реакции. Для расчета тепловых эффектов используются стандартные теплоты образования веществ. Стандартной теплотой (энтальпией) образования вещества ( или ) называется изменение энтальпии при образовании 1-го моля вещества из простых веществ, находящихся при стандартных условиях. Стандартная энтальпия простого вещества равна нулю.

Например, если вещество получено по реакции выраженной термохимическим уравнением

Ca_(тв.) + C_{(графит)} + 1,5O_2(газ) = CaCO_3(тв.) + 1207,7 Дж/моль,

его стандартная теплота образования равна

∆Hº_f,298 (CaCO₃)= - 1207,7 Дж/моль.

Третье следствие из закона Гесса: тепловой эффект реакции равен сумме теплот сгорания исходных веществ за вычетом (минус) суммы теплот сгорания продуктов реакции.

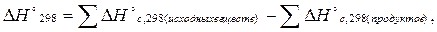
здесь индекс с от лат. combustum - сгорание.

Например для реакции aA + bB→cC + dD,

∆H₂₉₈ = a∆Hº_с,298(A) + b∆Hº_с,298(B) - c∆Hº_с,298(C) - d∆Hº_с,298(D)

Стандартная теплота сгорания вещества (∆Hº_с,298, ∆Hº_сгор. ) – это убыль энтальпии в реакции сгорания 1-го моля простого вещества или соединения, до соответствующих окисленных форм элементов. В случае сгорания соединений, состоящих из углерода и водорода (например, топливо) до CO₂ и H₂O. Стандартные теплоты сгорания и образования приведены в справочных таблицах термодинамических величин.

Закон Кирхгоффа устанавливает зависимость теплового эффекта реакции от температуры. Формулировка закона: температурный коэффициент теплового эффекта реакции равен изменению теплоемкости в результате процесса.

При изобарных условиях (Р=const)

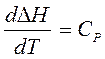, где .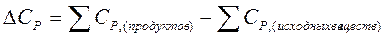

В зависимости от знака ∆C_Р тепловой эффект реакции (процесса) с ростом температуры может увеличиваться или уменьшаться.

1) Если ∆Cp >0, то с ростом температуры ∆H увеличивается.

2) Если ∆Cp <0, то с ростом температуры ∆H уменьшается

3) Если ∆Cp = 0, то тепловой эффект не зависит от температуры.

Проинтегрируем уравнение Кирхгоффа d∆H = ∆C_РdT.

1. Пусть теплоемкость С_Р не зависит от температуры, т.е. ∆С_Р = const, что допустимо в небольшом интервале температур. Тогда

. Отсюда выведем

формулу для вычисления теплового эффекта:

∆H₂ =∆H₁ + ∆C_Р(T₂ – T₁).

2. Пусть теплоемкость ∆C_Р – является функцией от температуры, т.е. ∆Cp= f(T). Эта зависимость выражается уравнениями Cp = a + bT + cT² или Cp = a + bT + 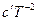. В общем виде изменение теплоемкости равно

∆Cp = ∆a + ∆bT + ∆cT² + . Подставим это выражение в уравнение Кирхгоффа, тогда

d∆HT = (∆aT + ∆bT + ∆cT² + 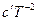)dT.

Возьмем неопределённый интеграл и получим выражение

.

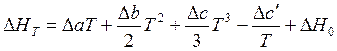Это уравнение показывает зависимость теплового эффекта реакции от температуры. В нем ∆H₀ – (2) определяемая как значение теплового эффекта при одной из температур.(1) постоянная интегрирования,

Закон Кирхгоффа для изохорного процесса (V=const) математически выражается как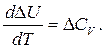

Лекция 4 (3 часа)

Второй закон термодинамики

План лекции: Второй закон термодинамики, его формулировки. Самопроизвольные (спонтанные) и несамопроизвольные процессы. Аналитическое выражение второго закона термодинамики и его обоснование с использованием цикла Карно. Энтропия. Объединенное уравнение первого и второго законов термодинамики. Расчет изменения энтропии в простейших термодинамических процессах - адиабатическом, изотермическом, изохорическом и изобарическом. Абсолютное значение энтропии. Постулат Планка. Изменение энтропии при фазовых переходах. Использование энтропии для определения направления протекания самопроизвольных процессов в изолированных системах.

Самопроизвольные процессы описываются следующими характеристиками.

1. Все природные самопроизвольные процессы протекают в одном направлении, т. е. имеют одностороннее направление. Например, тепло от горячего тела переходит к холодному; газы стремятся занять наибольший объём.

2. Часть энергии переходит в теплоту, т. е. система из упорядоченного состояния переходит в состояние с беспорядочным тепловым движением частиц.

3. Самопроизвольные процессы можно использовать для получения полезной работы. По мере превращения система теряет способность производить работу. В конечном состоянии равновесия она имеет наименьший запас энергии.

4. Систему нельзя вернуть в исходное состояние, не производя каких-либо изменений в ней самой или в окружающей среде. Все самопроизвольные процессы термодинамически необратимы.

5. В самопроизвольном процессе начальное состояние является менее вероятным по сравнению с каждым последующим и наименее вероятным по сравнению с конечным.

Термодинамическая вероятность характеризует ту или иную степень беспорядка в сообществе частиц, из которых состоят тела системы. Термодинамическая вероятность, или вероятность состояния системы, оценивается энтропией. Энтропия S – это особая функция состояния системы, связанная с теплотой:

,

где W - термодинамическая вероятность, определяемая как число микросостояний присущих данному макросостоянию; k – постоянная Больцмана; 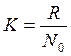, здесь N₀ – число Авогадро, равное 6,02 * 10²³.

Несамопроизвольные процессы протекают при затрате работы; при этом система удаляется от состояния равновесия (например, сжатие газа, электролиз).

Второй закон термодинамики – это постулат. Он имеет статистический характер и применим к системам из большого числа частиц. Второй закон термодинамики имеет следующие формулировки.

1. Теплота не может переходить самопроизвольно от менее нагретого тела к более нагретому.

2. Невозможен процесс, единственным результатом которого является превращение теплоты в работу.

3. Вечный двигатель второго рода невозможен.

Второй закон термодинамики выражается математически через изменение энтропии обратимого процесса следующим образом:

,

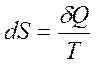где S – энтропия, это такая функция состояния системы, полный дифференциал которой в обратимом процессе равен отношению бесконечно малого количества теплоты к температуре.

Изменение энтропии в обратимом процессе равно изменению энтропии в необратимом процессе, т.е. 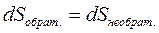. Сравним теплоты обратимого и необратимого процессов. Согласно первому закону термодинамики 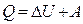. Внутренняя энергия U – это функция состояния системы, поэтому 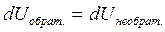. Максимальная работа совершается при обратимом процессе, поэтому 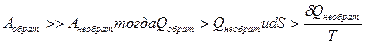. В общем случае для обратимого и необратимого процессов выражение второго закона термодинамики имеет следующее математическое выражение:

.

Здесь dS = const, а изменяется только правая часть уравнения, т.е. значение величины теплоты. Единицы измерения энтропии: [S] = Дж/моль *К.

Энтропия, как критерий возможности протекания процесса в изолированной системе (U,V=const). Изолированная система не обменивается с окружающей средой теплотой, т.е. 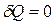. Поэтому, согласно второго закона термодинамики (dS)_U,V ≥ 0.

Необратимый процесс в изолированной системе возможен при

(dS)_U,V >0. При равновесном состоянии системы (или обратимом процессе) (dS)_U,V = 0; при этом энтропия принимает максимальное значение S=S_max. Если (dS)_U,V < 0 – необратимый процесс в изолированной системе неосуществим.

Рассмотрим вычисление изменения энтропии в различных процессах.

1. Изменение энтропии 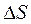при фазовых переходах (T=const) определяется по формуле

,

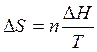где ∆H - теплота фазового перехода (кипение, испарение, возгонка, плавление); n – число молей вещества, переходящего из одной фазы в другую; n=g/M, где g – масса вещества, M – его молярная масса.

2. Изменение энтропии ∆S при нагревании.

а) Пусть p=const, тогда

, .

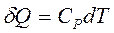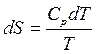Если C_Р=const, тогда ∆S = C_Р * ln,

где Т₁ и Т₂ – температуры начала и окончания нагревания вещества.

Пусть [ C_Р ] выражается в Дж/моль*К, тогда ∆S = n * C_Р * ln,

Пусть Cp выражается в Дж/г*К, тогда ∆S = C_Р * g * ln.

Если Cp зависит от температуры, т.е. C_Р = f(T), тогда

.

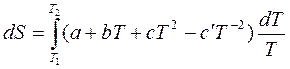б) Пусть V= const, тогда .

3. Измерение стандартной энтропии системы при протекании химической реакции определяется как разность суммы стандартных энтропий продуктов и суммы стандартных энтропий исходных веществ.

.

Значение величин стандартных энтропий веществ приведены в справочниках.

Постулат Планка имеет следующую формулировку: при абсолютном нуле энтропия правильно образованных кристаллов чистых веществ равна нулю. Постулат позволяет рассчитать абсолютное значение энтропии, если известны теплоты фазовых переходов, и если известны теплоёмкости вещества в различных агрегатных состояниях. Для расчёта абсолютного значения S вещество нагревается от абсолютного нуля до данной температуры.

Для твёрдого тела при температуре T

.

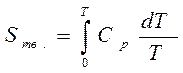Для жидкости при температуре T

Для газа при температуре T

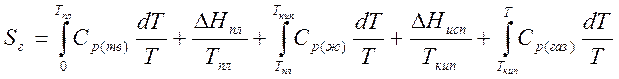
Дата добавления: 2014-01-07